题目内容
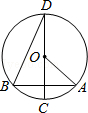
如图,在⊙O中,直径AB的长为10cm,弦AC=6cm,∠ACB的平分线CD交⊙O于点D.
(1)求BC、AD的长;(2)求四边形ADBC的面积.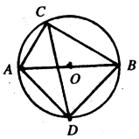
(1)求BC、AD的长;(2)求四边形ADBC的面积.

(1)∵AB是⊙O的直径,∴∠ACB=90°
在Rt△ABC中,AB=10cm,AC=6cm,由勾股定理得BC=8cm
∵CD平分∠ACB,∴∠ACD=∠BCD, ∴AD=BD
∴△ABD是等腰直角三角形.∴AD=5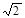
(2)S四边形ADBC=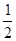 ×AC×BC+
×AC×BC+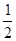 ×AD2=
×AD2=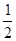 ×6×8+
×6×8+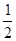 ×(5
×(5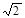 )2=49.
)2=49.
在Rt△ABC中,AB=10cm,AC=6cm,由勾股定理得BC=8cm
∵CD平分∠ACB,∴∠ACD=∠BCD, ∴AD=BD
∴△ABD是等腰直角三角形.∴AD=5
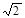
(2)S四边形ADBC=
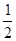 ×AC×BC+
×AC×BC+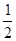 ×AD2=
×AD2=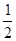 ×6×8+
×6×8+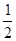 ×(5
×(5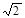 )2=49.
)2=49.(1)根据直径得出∠ACB=∠ADB=90°,根据勾股定理求出BC,根据圆周角定理求出AD=BD,根据勾股定理求出AD;
(2)根据三角形的面积公式,求出△ACB和△ADB的面积,相加即可求出答案.
(2)根据三角形的面积公式,求出△ACB和△ADB的面积,相加即可求出答案.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。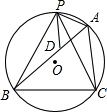
 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度; 的长度;
的长度;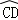 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;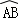 与
与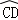 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.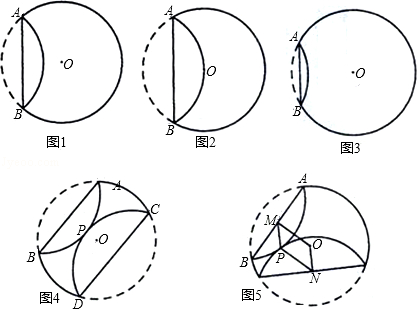

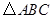 中,
中,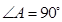 ,
,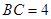 cm,分别以B、C为圆心的两个等圆外切,则图中阴影部分的面积为
cm,分别以B、C为圆心的两个等圆外切,则图中阴影部分的面积为 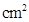 .
.