��Ŀ����
����Ŀ�����Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı�������
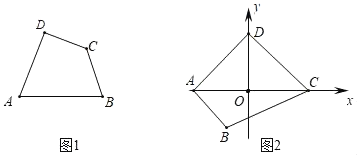
��1����֪����ͼ1���ı���ABCD�����ȶԽ��ı���������A����C����A��75������D��85�������C���� ����
��2����֪�������ȶԽ��ı�����ABCD�У���DAB��60������ABC��90����AB��4��AD��3����Խ���AC�ij���
��3����֪����ͼ2����ƽ��ֱ������ϵxOy�У��ı���ABCD�����ȶԽ��ı�����������A����2��0����C��2��0����B����1����![]() ������D��y���ϣ�������y��ax2+bx+c��a��0������A��D���ҵ���2��x��2ʱ������y��ax2+bx+cȡ���ֵΪ3���������ϵ��a��ֵ��
������D��y���ϣ�������y��ax2+bx+c��a��0������A��D���ҵ���2��x��2ʱ������y��ax2+bx+cȡ���ֵΪ3���������ϵ��a��ֵ��
���𰸡���1��115������2��AC�ij�Ϊ![]() ��
��![]() ����3��a����
����3��a����![]() ��1��
��1��![]()
��������
��1����B=��D=85�������C=360��-2��85��-75��=115����������⣻
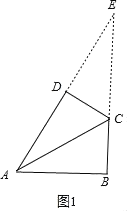
��2������ͼ1��![]() AE=8��DE=5�������
AE=8��DE=5�������![]() ����AC�����������ͼ2��ͬ���ɵ�
����AC�����������ͼ2��ͬ���ɵ�![]() BC=BF+CF
BC=BF+CF![]() �����ɹ��ɶ��������AC�ij���
�����ɹ��ɶ��������AC�ij���
��3���������ɵó���ADC=��ABC=90�������D��0��2��������A��D��������꣬����������ߵĽ���ʽΪy=ax2+��2a+1��x+2��������������ǣ���x=2ʱ������y=ax2+��2a+1��x+2ȡ�����ֵΪ3�������![]() ����-2��x��2ʱ���ڶ��㴦ȡ�����ֵ�������
����-2��x��2ʱ���ڶ��㴦ȡ�����ֵ�������![]()
�⣺��1����B����D��85�������C��360����2��85����75����115����
�ʴ�Ϊ115����
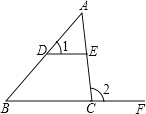
��2������ͼ1����B����D��90��ʱ���ӳ�AD��BC���ڵ�E��
�ߡ�DAB��60����
���E��30����
�֡�AB��4��AD��3
��BE��4![]() ��AE��8��DE��5��
��AE��8��DE��5��
��![]() ��
��
��BC��BE��CE��4![]() ��
��![]() ��
��
��![]() ��
��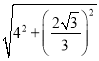 ��
��![]() ��
��
����ͼ����A����C��60��ʱ����D�ֱ���DE��AB��E��DF��BC�ڵ�F��
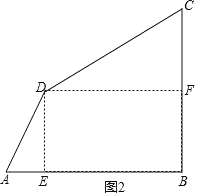
�ߡ�DAB����BCD��60����
�֡�AB��4��AD��3��
��![]() ��DE��BF��
��DE��BF��![]() ��
��
��![]() ��
��
��![]() ��
��
��BC��CF+BF��![]() ��
��
��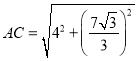 ��
��![]() ��
��
�ۺ����Ͽɵ�AC�ij�Ϊ![]() ��
��![]() ��
��
��3����A����2��0����C��2��0����B����1����![]() ����
����
��AB��2��BC��2![]() ��AC��4��
��AC��4��
��AB2+BC2��AC2��
���ABC��90����
��AD��CD��AB��BC��
���BAD����BCD��
���ı���ABCD�����ȶԽ��ı�����
���ADC����ABC��90����
��D��0��2��
��������y��ax2+bx+c����A����2��0����D��0��2����
��![]() ��
��
��ã�c��2��b��2a+1��
�������ߵĽ���ʽΪy��ax2+��2a+1��x+2��
��x��2ʱ������y��ax2+��2a+1��x+2ȡ�����ֵΪ3��
��4a+4a+2+2��3��
��a����![]() ��
��
��ʱ�����ߵĶԳ���Ϊx��3��
��![]() �������⣬
�������⣬
�����κ���y��ax2+��2a+1��x+2�ڶ���ȡ�����ֵ3�����У�
![]() ��
��
��ã�a����1+![]() ��a����1��
��a����1��![]() ��
��
��a����1+![]() ʱ���Գ�����ֱ��x��2���Ҳ࣬�������⣬��ȥ��
ʱ���Գ�����ֱ��x��2���Ҳ࣬�������⣬��ȥ��
��![]() ��
��
�ۺ����Ͽɵ�a����![]() ��1��
��1��![]() ��
��

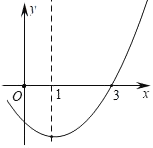
����Ŀ����֪���κ���y��ax2+b��ͼ����ֱ��y��x+2�ཻ�ڵ�A��1��m������B��n��0����
��1������κ����Ľ���ʽ����д���Ò����ߵĶԳ���Ͷ������ꣻ
��2��ѡȡ�ʵ������������±�������ͼ�е�ֱ������ϵ����㻭���������ߵ�ͼ��
x | ���� | �� �� | �� �� | �� �� | �� �� | �� �� | ���� |
y | ���� | �� �� | �� �� | �� �� | �� �� | �� �� | ���� |
��3������������������ͼ�����ͼ��ֱ��д��ax2+b��x+2ʱx��ȡֵ��Χ��