题目内容
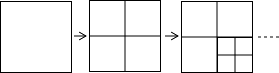
【题目】已知,在矩形ABCD中,连接对角线AC,将△ABC绕点B顺时针旋转90°得到△EFG,并将它沿直线AB向左平移,直线EG与BC交于点H,连接AH,CG.
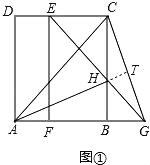
(1)如图①,当AB=BC,点F平移到线段BA上时,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想;
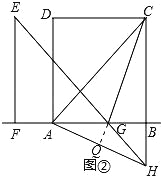
(2)如图②,当AB=BC,点F平移到线段BA的延长线上时,(1)中的结论是否成立,请说明理由;
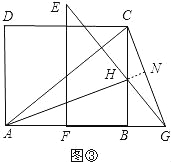
(3)如图③,当AB=nBC(n≠1)时,对矩形ABCD进行如已知同样的变换操作,线段AH,CG有怎样的数量关系和位置关系?直接写出你的猜想.

【答案】(1) AH=CG,AH⊥CG ;(2) 仍然成立,理由详见解析;(3) AH=nCG,AH⊥CG.理由详见解析.
【解析】
试题分析:(1)延长AH与CG交于点T,如图①,易证BH=BG,从而可证到△ABH≌△CBG,则有AH=CG,∠HAB=∠GCB,从而可证到∠HAB+∠AGC=90°,进而可证到AH⊥CG.
(2)延长CG与AH交于点Q,如图②,仿照(1)中的证明方法就可解决问题.
(3)延长AH与CG交于点N,如图③,易证BH∥EF,可得△GBH∽△GFE,则有![]() ,也就有
,也就有![]() ,从而可证到△ABH∽△CBG,则有
,从而可证到△ABH∽△CBG,则有![]() =n,∠HAB=∠GCB,进而可证到AH=nCG,AH⊥CG.
=n,∠HAB=∠GCB,进而可证到AH=nCG,AH⊥CG.
试题解析:(1)AH=CG,AH⊥CG.
证明:延长AH与CG交于点T,如图①,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=BC,
∴EF=GF,∠EFG=∠ABC=90°.
∴∠CBG=90°,∠EGF=45°.
∴∠BHG=90°﹣45°=45°=∠EGF.
∴BH=BG.
在△ABH和△CBG中,
AB=BC,∠ABH=∠CBG,BH=BG,
∴△ABH≌△CBG(SAS).
∴AH=CG,∠HAB=∠GCB.
∴∠HAB+∠AGC=∠GCB+∠AGC=90°.
∴∠ATC=90°.
∴AH⊥CG.
(2)(1)中的结论仍然成立.
证明:延长CG与AH交于点Q,如图②,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=BC,
∴EF=GF,∠EFG=∠ABC=90°.
∴∠ABH=90°,∠EGF=45°.
∴∠BGH=∠EGF=45°.
∴∠BHG=90°﹣45°=45°=∠BGH.
∴BH=BG.
在△ABH和△CBG中,
AB=BC,∠ABH=∠CBG,BH=BG,
∴△ABH≌△CBG(SAS).
∴AH=CG,∠HAB=∠GCB.
∴∠GCB+∠CHA=∠HAB+∠CHA=90°.
∴∠CQA=90°.
∴CG⊥AH.
(3)AH=nCG,AH⊥CG.理由如下:
延长AH与CG交于点N,如图③,
由旋转和平移的性质可得:EF=AB,FG=BC,∠EFG=∠ABC.
∵四边形ABCD是矩形,AB=nBC,
∴EF=nGF,∠EFG=∠ABC=90°.
∴∠EFG+∠ABC=180°.
∴BH∥EF.
∴△GBH∽△GFE.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵∠ABH=∠CBG,
∴△ABH∽△CBG.
∴![]() =n,∠HAB=∠GCB.
=n,∠HAB=∠GCB.
∴AH=nCG,∠HAB+∠AGC=∠GCB+∠AGC=90°.
∴∠ANC=90°.
∴AH⊥CG.

【题目】2016年2月上旬福州地区空气质量指数(AQI)如下表所示,空气质量指数不大于100表示空气质量优良,如果小王该月上旬来福州度假三天那么他在福州度假期间空气质量都是优良的概率是 .
2016年2月上旬福州地区空气质量指数(AQI)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ug/m3 | 26 | 34 | 43 | 41 | 34 | 48 | 78 | 1 15 | 59 | 45 |