��Ŀ����
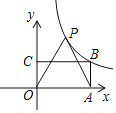
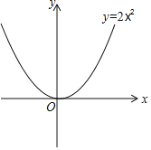
����Ŀ����ͼ����֪������OABC�����Ϊ9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B�ں���y��![]() (k��0��x��0)��ͼ���ϣ���P(m��n)�Ǻ���y��
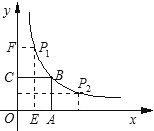
(k��0��x��0)��ͼ���ϣ���P(m��n)�Ǻ���y��![]() (k��0��x��0)��ͼ������һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS.
(k��0��x��0)��ͼ������һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS.

(1)���B�������k��ֵ��
(2)��S��![]() ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
(3)д��S����m�ĺ�������ʽ��
���𰸡���1����3,3����![]() ��2��
��2��![]() ��
��![]() ��3��
��3��![]() ��
��![]()
��������
��1�����ݷ����������������ε�����뷴����ϵ���Ĺ�ϵ��������÷�������������ʽ���������B�����ꣻ
��2������������ֱ����.
��3������(2)����д����������ʽ��
�⣺(1)��������OABC�����Ϊ9��
��OA=OC=3��
��B(3,3).
�֡ߵ�B(3,3)�ں���![]() (k>0,x>0)��ͼ���ϣ�
(k>0,x>0)��ͼ���ϣ�
��k=9.
(2)������������ٵ���P1�ڵ�B�����ʱ��
��P1(m,n)�ں���![]() �ϣ�
�ϣ�
��mn=9.
����![]()
��![]()
��n=6.
��![]()
�ڵ���P2�ڵ�B��B���Ҳ�ʱ��
��P2(m,n)�ں���![]() �ϣ�
�ϣ�
��mn=9.
��![]()
��n=![]() ��
��
��m=6.
��![]()
(3)��0<m<3ʱ��![]() 93m��
93m��
��![]() ʱ��
ʱ�� ![]()
��n=![]()
![]()
![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ