题目内容
【题目】已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m),点B(n,0).
(1)求二次函数的解析式,并写出该拋物线的对称轴和顶点坐标;
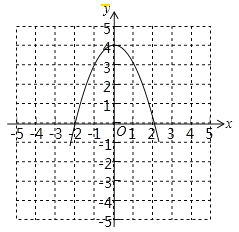
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线的图象;
x | …… |
|
|
|
|
| …… |
y | …… |
|
|
|
|
| …… |
(3)画出这两个函数的图象,并结合图象直接写出ax2+b>x+2时x的取值范围.

【答案】(1)对称轴为x=0,顶点为(0,4);(2)见解析;(3)见解析,﹣2<x<1.
【解析】
(1)求出A、B的坐标,利用待定系数法联立方程组即可求二次函数的解析式;
(2)利用描点法画出函数解析式;
(3)将二次函数与一次函数同时画在一个坐标系内,由图象即可求解.
(1)将点A(1,m)、点B(n,0)代入直线y=x+2,∴m=3,n=﹣2,∴点A(1,3),点B(﹣2,0),将点A、B分别代入二次函数y=ax2+b,得到![]() ,∴
,∴![]() ,∴y=﹣x2+4,∴对称轴为x=0,顶点为(0,4);
,∴y=﹣x2+4,∴对称轴为x=0,顶点为(0,4);
(2)
 画图见解析:
画图见解析:
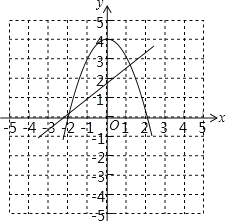
(3)如图,由图象可得ax2+b>x+2时,﹣2<x<1.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目