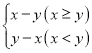Question

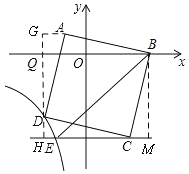
【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为(l,1)，点B在x轴正半轴上，点D在第三象限的双曲线y=上，过点C作CE//x轴交双曲线于点E，连接BE，则△BCE的面积为________．

Answer 1

【答案】7

【解析】

作辅助线，构建全等三角形：过D作GH⊥x轴，过A作AG⊥GH，过B作BM⊥HC于M，证明△AGD△DHC△CMB，根据点D的坐标表示：AG=DH=x1，由DG=BM，列方程可得x的值，表示D和E的坐标，根据三角形面积公式可得结论．

过D作GH⊥x轴，过A作AG⊥GH，过B作BM⊥HC于M，

设D(x,)，

∵四边形ABCD是正方形，

∴AD=CD=BC，∠ADC=∠DCB=90°，

易得△AGD△DHC△CMB，

∴AG=DH=x1，

∴DG=BM，

∴1=1x，

x=2，

∴D(2,3)，CH=DG=BM=1=4，

∵AG=DH=1x=1，

∴点E的纵坐标为4，

当y=4时，x=，

∴E(-,4)，

∴EH=2=，

∴CE=CHHE=4=，

∴S△CEB=CEBM=××4=7