题目内容
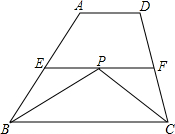
如图,在等腰梯形ABCD中,AD∥BC,AE⊥BC于点E.DF⊥BC于点F.AD=2cm,BC=6cm,AE=4cm.点P、Q分别在线段AE、DF上,顺次连接B、P、Q、C,线段BP、PQ、QC、CB所围成的封闭图形记为M,若点P在线段AE上运动时,点Q也随之 在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题:
在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题:
(1)直接写出当x=3时y的值;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)当x取何值时,图形M成为等腰梯形?图形M成为三角形?
(4)直接写出线段PQ在运动过程中所能扫过的区域的面积.
 在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题:
在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2,设EP=xcm,FQ=ycm.解答下列问题:(1)直接写出当x=3时y的值;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)当x取何值时,图形M成为等腰梯形?图形M成为三角形?
(4)直接写出线段PQ在运动过程中所能扫过的区域的面积.
(1)由等腰梯形的性质得:BE=EF=FC=2,
∴SM=S△BPE+S△QFC+S梯形QFEP
=
BE•x+
FC•y+
•EF
=
×2x+
×2y+
×2
=2(x+y),
把SM=10,x=3代入上式,解得y=2.
(2)由等腰梯形的性质得:BE=EF=FC=2,
∵S△BEP+S梯形PEFQ+S△FCQ=S梯形M,
∴
×2x+
(x+y)×2+
×2y=10,
∴y=-x+5,
由
,得1≤x≤4.
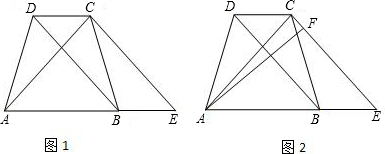
(3)若图形M为等腰梯形(如图1),则EP=FQ,即x=-x+5,解得x=
.
∴当x=
时,图形M为等腰梯形.
若图形M为三角形,分两种情形:
①当点P、Q、C在一条直线上时(如图2),EP是△BPC的高,
∴
BC•EP=10,即
×6x=10,解得x=
;
②当点B、P、Q在一条直线上时(如图3),FQ是△BQC的高,
∴
BC•FQ=10,即
×6×(-x+5)=10,解得x=
;
∴当x=
或
时,图形M为三角形.
(4)线段PQ扫过的部分是两个全等的三角形,且都是以x最小时AP的长为底,
AD的长为高,在(2)中已经求得x的取值范围为1≤x≤4,所以此时AP=AE-xmin=3,那么线段PQ扫过的面积即为:2S=2×
×3×1=3cm2;
评分说明:(4)中不写单位不扣分,线段PQ在运动过程中所能扫过的区域为图4中阴影部分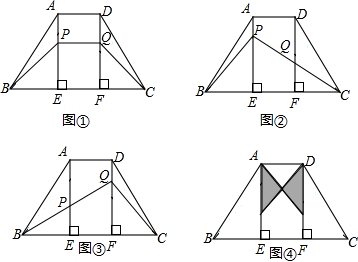
∴SM=S△BPE+S△QFC+S梯形QFEP
=
| 1 |
| 2 |
| 1 |
| 2 |
| x+y |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| x+y |
| 2 |
=2(x+y),
把SM=10,x=3代入上式,解得y=2.
(2)由等腰梯形的性质得:BE=EF=FC=2,
∵S△BEP+S梯形PEFQ+S△FCQ=S梯形M,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴y=-x+5,
由
|
(3)若图形M为等腰梯形(如图1),则EP=FQ,即x=-x+5,解得x=
| 5 |
| 2 |
∴当x=
| 5 |
| 2 |
若图形M为三角形,分两种情形:
①当点P、Q、C在一条直线上时(如图2),EP是△BPC的高,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
②当点B、P、Q在一条直线上时(如图3),FQ是△BQC的高,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
∴当x=
| 10 |
| 3 |
| 5 |
| 3 |
(4)线段PQ扫过的部分是两个全等的三角形,且都是以x最小时AP的长为底,
| 1 |
| 2 |
| 1 |
| 2 |
评分说明:(4)中不写单位不扣分,线段PQ在运动过程中所能扫过的区域为图4中阴影部分


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目