题目内容
有四根木棒的长度分别为3cm，5cm，6cm，8cm，在平面内首尾相接围成一个梯形区域，梯形区域的面积是（ ）
A．
| B．55cm2 | ||
| C．66cm2 | D．55cm2或66cm2 |
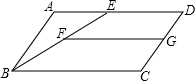
根据题意，梯形的两底长分别为3cm和8cm，腰分别为5cm和6cm，如图所示，AD=3，BC=8，AB=5，CD=6．作DE∥AB于点E，EF⊥CD于F，DH⊥BC于H．
∵AD∥BC，DE∥AB，∴四边形ABED是平行四边形．
∴DE=AB=5，BE=AD=3，EC=8-3=5．
∴DE=EC．即△CDE为等腰三角形．
∵EF⊥CD，CD=6，
∴CF=3．∴EF=4．
S△CDE=
CD•EF=
EC•DH，
即5•DH=24，∴DH=
．
所以梯形面积=
×（3+8）×
=
（cm2）．
故选A．
∵AD∥BC，DE∥AB，∴四边形ABED是平行四边形．
∴DE=AB=5，BE=AD=3，EC=8-3=5．
∴DE=EC．即△CDE为等腰三角形．
∵EF⊥CD，CD=6，
∴CF=3．∴EF=4．
S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
即5•DH=24，∴DH=
| 24 |
| 5 |
所以梯形面积=
| 1 |
| 2 |
| 24 |
| 5 |
| 132 |
| 5 |
故选A．
练习册系列答案
相关题目
在线段DF上运动，使图形M的形状发生改变，但面积始终为10cm2，设EP=xcm，FQ=ycm．解答下列问题：
