题目内容
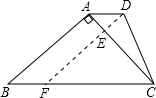
如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．
如图，过点D作DF∥AB，分别交AC，BC于点E，F．（1分）
∵AB⊥AC，
∴∠AED=∠BAC=90度．
∵AD∥BC，
∴∠DAE=180°-∠B-∠BAC=45度．
在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×
=2
（2分）
在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=
．∴CE=AC-AE=
．（4分）
在Rt△DEC中，∠CED=90°，∴DC=
=
．（5分）
∵AB⊥AC，
∴∠AED=∠BAC=90度．
∵AD∥BC，
∴∠DAE=180°-∠B-∠BAC=45度．
在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×
| ||
| 2 |
| 2 |
在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=
| ||
| 2 |
| 3 |
| 2 |
| 2 |
在Rt△DEC中，∠CED=90°，∴DC=
| DE2+CE2 |
| 5 |
练习册系列答案
出彩同步大试卷系列答案
相关题目
在线段DF上运动，使图形M的形状发生改变，但面积始终为10cm2，设EP=xcm，FQ=ycm．解答下列问题：
向B点运动．当Q点到达B点时，动点P、Q同时停止运动．设点P、Q同时出发，并运动了t秒，
