题目内容
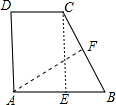
如图，在直角梯形ABCD中，底AB=13，CD=8，AD⊥AB并且AD=12，则A到BC的距离为（ ）
| A．12 | B．13 | C．
| D．10.5 |
如图，作CE⊥AB交点为E，作AF⊥BC交点为F．
∵在直角梯形ABCD中，AD⊥AB，CE⊥AB，
∴DC=AE=8，AD=CE=12，则BE=AB-AE=13-8=5，
∴在直角三角形BCE中，BC=
=13．即可得AB=CB；
∵∠CEB=∠AFB=90°，∠B为公共角，AB=CB，
∴△AFB≌△CEB（AAS），
∴CE=AF=12．
故选A．
∵在直角梯形ABCD中，AD⊥AB，CE⊥AB，
∴DC=AE=8，AD=CE=12，则BE=AB-AE=13-8=5，
∴在直角三角形BCE中，BC=
| CE2+BE2 |
∵∠CEB=∠AFB=90°，∠B为公共角，AB=CB，
∴△AFB≌△CEB（AAS），
∴CE=AF=12．
故选A．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
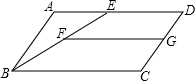
在线段DF上运动，使图形M的形状发生改变，但面积始终为10cm2，设EP=xcm，FQ=ycm．解答下列问题：