Question

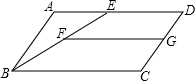
如图甲，四边形ABCD是等腰梯形，AB∥DC．由4个这样的等腰梯形可以拼出图乙所示的平行四边形．
（1）求梯形ABCD四个内角的度数；
（2）试探梯形ABCD四条边之间存在的数量关系，并说明理由．

Answer 1

（1）如图∠1=∠2=∠3，∠1+∠2+∠3=360°，即∠1=120°，所以图甲中梯形的上底角均为120°，下底角均为180°-120°=60°．

（2）∵EF既是梯形的腰，又是梯形的上底，
∴梯形的腰等于上底，即MF=FN=EF，
连接MN，
∵∠3=120°，MF=FN，
∴∠FMN=∠FNM=

180°-∠3

2

=

180°-120°

2

=30°，
∴∠HMN=30°，∠HNM=90°，
∴NH=

1

2

MH，因此梯形的上底等于下底长的一半，且等于腰长．