��Ŀ����
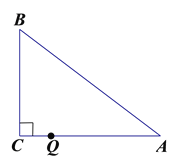
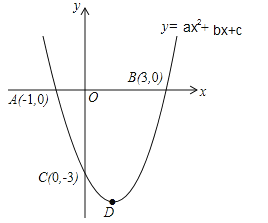
����Ŀ����ͼ����Rt��ABC�У�![]() ������һ�㹻���ֱ�����ǰ壬����ֱ�Ƕ���D��BC����һ�㣬������ֱ�DZ߷ֱ�AB��AC�ڵ�E��F.
������һ�㹻���ֱ�����ǰ壬����ֱ�Ƕ���D��BC����һ�㣬������ֱ�DZ߷ֱ�AB��AC�ڵ�E��F.

��1����ͼ1����DE��AB��DF��AC����֤���ı���AEDF�Ǿ���
��2���ڣ�1�������£�����D�ڡ�BAC�Ľ�ƽ�����ϣ����жϴ�ʱ�ı���AEDF��״����˵�����ɣ�
��3������D�ڡ�BAC�Ľ�ƽ�����ϣ���ֱ�����ǰ��Ƶ�D��תһ���ĽǶȣ�ʹ��ֱ�����ǰ��������������ֱ�DZ߷ֱ��ڵ�E��F����ͼ2������֤��![]() .�������������ߣ�
.�������������ߣ�
���𰸡���1�������� ��2�������Σ����ɼ����� ��3��������
��������
��1���ɴ�ֱ�Ķ���õ���AED=��AFD=90�������ݾ��ε��ж��������ɵõ����ۣ�
��2�����ݽ�ƽ���ߵ����ʵõ�DE=DF�����������ε��ж��������ɵõ�����AEDF�������Σ�
��3����DM��AB��M��DN��AC��N��֤���ı���AMDN�������Σ��������ε����ʵõ�AM=DM=DN=AN����MDN=��AMD=90��������ǵ����ʵõ���NDF=��EDM������ȫ�������ε����ʵõ�EM=FN�����ݹ��ɶ����õ�AD=![]() AM������AM=
AM������AM=![]() ��AM+AN��=
��AM+AN��=![]() ��AE+AF���������������ɵõ����ۣ�
��AE+AF���������������ɵõ����ۣ�
��1����DE��AB��BF��AC��
���AED=��AFD=90����
�ߡ�BAC=90����
���ı���AEDF�Ǿ��Σ�
��2���ı���AEDF�������Σ�
���ɣ��ߵ�D�ڡ�BAC�� ��ƽ�����ϣ�DE��AB��BF��AC��
��DE=DF��
�����AEDF��������
��3����DM��AB��M��DN��AC��N��
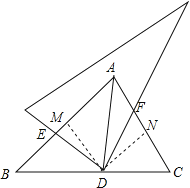
���AMD=��AND=��BAC=90����
�ߵ�D�ڡ�BAC�� ��ƽ�����ϣ�
��DM=DN��
���ı���AMDN�������Σ�
��AM=DM=DN=AN����MDN=��AMD=90����
���MDF+��NDF=90����
�ߡ�EDF=90����
���MDF+��EDM=90����
���NDF=��EDM��
����EMD����FND��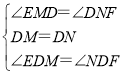 ��
��
���EMD�ա�FND��
��EM=FN��
�ߡ�AMD=90����
��AM2+DM2=AD2��
��AD=![]() AM��
AM��
��AM=![]() ��AM+AN��=
��AM+AN��=![]() ��AE+AF����
��AE+AF����
��AD=![]() ��
��![]() ��AE+AF����
��AE+AF����
��AE+AF=![]() AD��
AD��