题目内容
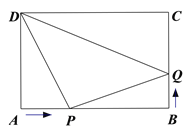
【题目】如图，△ABC中，∠C=90°，它的三边长是三个连续的正偶数，且AC＞BC.
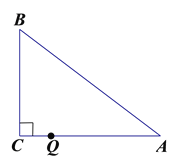
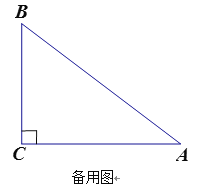
(1)这个直角三角形的各边长；
(2)若动点Q从点C出发，沿CA方向以1个单位长度/秒的速度运动，到达点A停止运动，请运用尺规作图作出以点Q为圆心，QC为半径，且与AB边相切的圆，并求出此时点Q的运动时间.
(3) 若动点Q从点C出发，沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动，以Q为圆心、QC长为半径作圆，请探究点Q在整个运动过程中，运动时间t为怎样的值时，⊙Q与边AB分别有0个公共点、1个公共点和2个公共点？
【答案】（1）6,8,10；（2）t=3；（3）当0＜t＜3时，⊙Q与边AB有0个公共点，
当t=3或4＜t≤8时，⊙Q与边AB有1个公共点，
当3＜t≤4时，⊙Q与边AB有2个公共点.
【解析】【试题分析】（1）根据直角△ABC的三边长是三个连续的正偶数，设最短的边为x，则另两边分别为x+2,x+4.根据勾股定理得：（x+4）2=x2+(x+2)2，解得x1=6,x2=-2（舍去），三边长分别是6,8,10.
（2）设⊙Q与AB相切与点P.根据切线的性质得：∠BPQ=90°,由于∠C=90°,根据切线的判定得，BC与⊙Q 相切，根据切线长定理得，BC=BP=6，AP=4
设CQ=x，则AQ=8-x在Rt
中，利用勾股定理得：AQ2=PQ2+AP2，即(8-x)2=x2+42
解得：x=3，即t=3
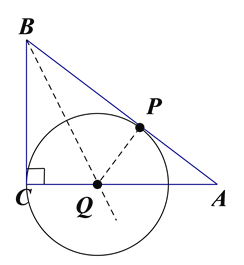
（3）根据（2）的求解，依据数形结合思想,易得：当0＜t＜3时，⊙Q与边AB有0个公共点；当t=3或4＜t≤8时，⊙Q与边AB有1个公共点；当3＜t≤4时，⊙Q与边AB有2个公共点.
【试题解析】
（1）设最短的边为x，则另两边分别为x+2,x+4.
根据题意，得：（x+4）2=x2+(x+2)2
整理得x2-4x-12=0，解得x1=6,x2=-2（舍去）
三边长分别是6,8,10.
（2）设⊙Q与AB相切与点P
∴∠BPQ=90°
∵∠C=90°
∴BC与⊙Q 相切
∴BC=BP=6
∴AP=4
设CQ=x，则AQ=8-x
∵AQ2=PQ2+AP2
∴(8-x)2=x2+42
∴x=3
即t=3
（3）当0＜t＜3时，⊙Q与边AB有0个公共点，
当t=3或4＜t≤8时，⊙Q与边AB有1个公共点，
当3＜t≤4时，⊙Q与边AB有2个公共点.
