题目内容
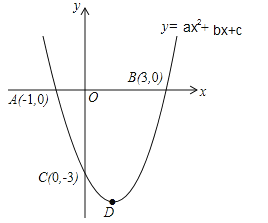
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴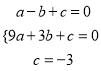 ,解得:
,解得: 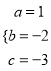 ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() );
);
②当DA=DP时, ![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当AD=AP时, ![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).

练习册系列答案
相关题目