题目内容
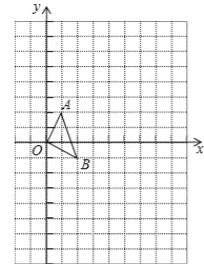
【题目】如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,﹣1).
(1)以点O(0,0)为位似中心,按位似比1:3在位似中心的同侧将△OAB放大为△OA′B′,放大后点A、B的对应点分别为A′、B′,请在图中画出△OA′B′;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C'的坐标____;
(3)直接写出四边形ABA′B′的面积是____.
【答案】 (3a,3b) 20
【解析】试题分析:(1)利用位似图形的性质得出对应点位置进而求出即可;
(2)利用位似图形的性质结合位似比进而求出即可;
(3)先后求出S△A′OB′、S△AOB,继而根据S四边形ABA′B′=S△A′OB′﹣S△AOB可得.
试题解析:解:(1)如图,△OA′B′即为所求作三角形;

(2)∵点A(1,2)的对应点A′的坐标:(3,6),点B(2,﹣1)的对应点B′的坐标:(6,﹣3);∴点C(a,b)的对应点C'的坐标为:(3a,3b);故答案为:(3a,3b);
(3)∵OA=OB=![]() ,AB=
,AB=![]() ,∴OA2+OB2=AB2,∴△AOB为等腰直角三角形,则S△AOB=
,∴OA2+OB2=AB2,∴△AOB为等腰直角三角形,则S△AOB=![]() OAOB=
OAOB=![]() ,同理可得S△A′OB′=
,同理可得S△A′OB′=![]() OA′OB′=
OA′OB′=![]() ,∴四边形ABA′B′的面积是S△A′OB′﹣S△AOB=20,故答案为:20.
,∴四边形ABA′B′的面积是S△A′OB′﹣S△AOB=20,故答案为:20.

练习册系列答案
相关题目
