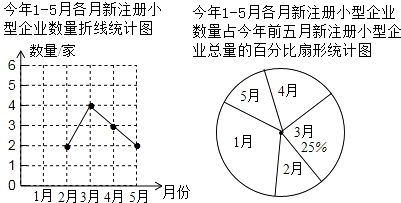
题目内容
【题目】已知:关于 x 的方程 2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及 k 值.
【答案】(1)证明见解析;(2)k=1,另外一根为![]() .
.
【解析】
试题若方程有两个不相等的实数根,则应有△=b2-4ac>0,故计算方程的根的判别式即可证明方程根的情况,第二小题可以直接代入x=-1,求得k的值后,解方程即可求得另一个根.
试题解析:(1)证明:∵a=2,b=k,c=-1
∴△=k2-4×2×(-1)=k2+8,
∵无论k取何值,k2≥0,
∴k2+8>0,即△>0,
∴方程2x2+kx-1=0有两个不相等的实数根.
(2)把x=-1代入原方程得,2-k-1=0
∴k=1
∴原方程化为2x2+x-1=0,
解得:x1=-1,x2=![]() ,
,
即另一个根为![]() .
.

练习册系列答案
相关题目