Question

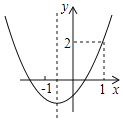
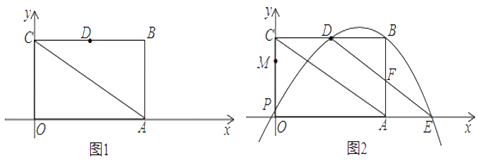
【题目】如图1，矩形OABC的顶点A的坐标为（4,0），O为坐标原点，点B在第一象限，连接AC， tan∠ACO=2，D是BC的中点，

（1）求点D的坐标；

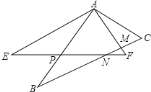
（2）如图2，M是线段OC上的点，OM=OC，点P是线段OM上的一个动点，经过P、D、B三点的抛物线交 轴的正半轴于点E，连接DE交AB于点F.

①将△DBF沿DE所在的直线翻折，若点B恰好落在AC上，求此时点P的坐标；

②以线段DF为边，在DF所在直线的右上方作等边△DFG，当动点P从点O运动到点M时，点G也随之运动，请直接写出点G运动的路径的长.

Answer 1

【答案】（1）D（2,2）；（2）①P（0,0）；②

【解析】

（1）根据三角函数求出OC的长度，再根据中点的性质求出CD的长度，即可求出D点的坐标；

（2）①证明在该种情况下DE为△ABC的中位线，由此可得F为AB的中点，结合三角形全等即可求得E点坐标，结合二次函数的性质可设二次函数表达式（此表达式为交点式的变形，利用了二次函数的平移的特点），将E点代入即可求得二次函数的表达式，根据表达式的特征可知P点坐标；

②可得G点的运动轨迹为，证明△DFF'≌△FGG'，可得GG'＝FF'，求得P点运动到M点时的解析式即可求出F'的坐标，结合①可求得FF'即GG'的长度.

解：（1）∵四边形OABC为矩形，

∴BC=OA=4，∠AOC=90°，

∵在Rt△ACO中，tan∠ACO==2，

∴OC=2，

又∵D为CB中点，

∴CD=2，

∴D（2,2）；

（2）①如下图所示，

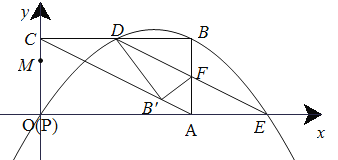
若点B恰好落在AC上的时,根据折叠的性质,

∵D为BC的中点，

∴CD=BD,

∴,

∴,

∴，

∴,DF为△ABC的中位线，

∴AF=BF,

∵四边形ABCD为矩形

∴∠ABC=∠BAE=90°

在△BDF和△AEF中，

∵

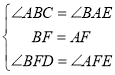
∴△BDF≌△AEF，

∴AE=BD=2,

∴E(6,0),

设，将E（6,0）带入，8a+2=0

∴a=，则二次函数解析式为，此时P（0,0）；

②如图，当动点P从点O运动到点M时，点F运动到点F'，点G也随之运动到G'．连接GG'．当点P向点M运动时，抛物线开口变大，F点向上线性移动，所以G也是线性移动．

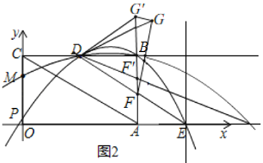
∵OM=OC=

∴,

当P点运动到M点时，设此时二次函数表达式为，将代入得，解得，所以抛物线解析式为，整理得.

当y=0时，，解得x=8（已舍去负值），

所以此时，

设此时直线 的解析式为y=kx+b，

将D（2,2），E（8,0）代入解得，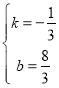

所以，

当x=4时，，所以,

由①得，

所以,

∵△DFG、△DF'G'为等边三角形，

∴∠GDF＝∠G'DF'＝60°，DG＝DF，DG'＝DF'，

∴∠GDF﹣∠GDF'＝∠G'DF'﹣∠GDF'，

即∠G'DG＝∠F'DF，

在△DFF'与△FGG'中，

，

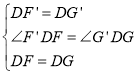∴△DFF'≌△FGG'（SAS），

∴GG'＝FF'，

即G运动路径的长为．