Question

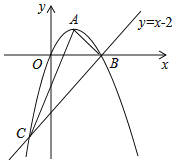
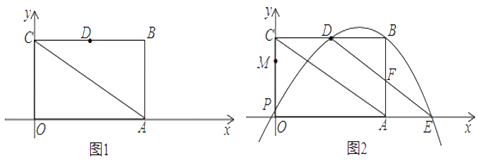
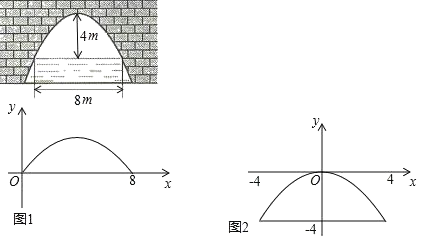
【题目】图中所示的抛物线形拱桥，当拱顶离水面4m时，水面宽8m．水面上升3米，水面宽度减少多少？下面给出了解决这个问题的两种建系方法．

方法一如图1，以上升前的水面所在直线与抛物线左侧交点为原点，以上升前的水面所在直线为x轴，建立平面直角坐标系xOy；

方法二如图2，以抛物线顶点为原点，以抛物线的对称轴为y轴，建立平面直角坐标系xOy，

Answer 1

【答案】4m

【解析】

方法一：根据顶点坐标为（4，4），设其解析式为y＝a（x﹣4）2+4，将（0，0）代入求出a的值即可得；

方法二：设抛物线解析式为y＝ax2，将点（4，﹣4）代入求得a的值，据此可得抛物线的解析式，再求出上涨3m后，即y＝﹣1时x的值即可得．

解：方法一、根据题意知，抛物线与x轴的交点为（0，0）、（8，0），其顶点坐标为（4，4），

设解析式为y＝a（x﹣4）2+4，

将点（0，0）代入，得：16a+4＝0，

解得：a＝﹣，

则抛物线解析式为y＝﹣（x﹣4）2+4＝﹣x2+2x，

当y＝3时，﹣x2+2x＝3，

解得：x＝2或x＝6，

则水面的宽减少了8﹣（6﹣2）＝4（m）．

方法二：由题意知，抛物线过点（4，﹣4），

设抛物线解析式为y＝ax2，

将点（4，﹣4）代入，得：16a＝﹣4，

解得：a＝﹣，

所以抛物线解析式为y＝﹣x2，

当y＝﹣1时，﹣x2＝﹣1，

解得：x＝2或x＝﹣2，

则水面的宽减少了8﹣4＝4（m）．