Question

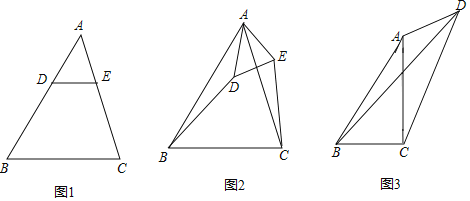
【题目】如图①，△ABC，△CDE都是等边三角形．

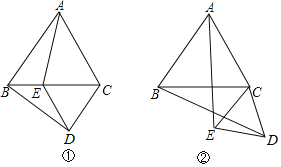
（1）写出AE与BD的大小关系.

（2）若把△CDE绕点C逆时针旋转到图②的位置时，上述（1）的结论仍成立吗？请说明理由．

（3）△ABC的边长为5，△CDE的边长为2，把△CDE绕点C逆时针旋转一周后回到图①位置，求出线段AE长的最大值和最小值．

Answer 1

【答案】（1）AE＝BD，理由见解析；（2）AE＝BD，理由见解析；（3）线段AE长的最大值为7，最小值3．

【解析】

（1）根据等边三角形的性质可得AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，利用SAS可证明△ACE≌△BCD，即可得AE=BD；

（2）根据等边三角形的性质可得AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，利用角的和差关系可得∠ACE＝∠BCD，利用SAS可证明△ACE≌△BCD，可得AE=BD；

（3）利用三角形三边关系即可得答案.

（1）AE＝BD，理由：

∵△ABC，△CDE都是等边三角形，

∴AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，

∴△ACE≌△BCD（SAS），

∴AE＝BD.

（2）AE＝BD，理由：

∵△ABC，△CDE都是等边三角形，

∴AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，

∴∠ACB+∠BCE＝∠DCE+∠BCE，

∴∠ACE＝∠BCD，

∴△ACE≌△BCD（SAS），

∴AE＝BD.

（3）∵△ABC的边长为5，△CDE的边长为2，

∴AC＝5，CE＝2，

在△ACE中，AC+CE＞AE，

∴当点E在AC的延长线上时，AE达到最大，最大值为AE＝AC+CE＝5+2＝7，

在△ACE中，AC﹣CE＜AE，

∴当点E在线段AC上时，AE达到最小AE＝AC﹣CE＝5﹣2＝3，

即：线段AE长的最大值为7，最小值3．