题目内容
【题目】如图，在平行四边形ABCD中，E为BC边上一点，连接DE，点F为线段DE上一点，且∠AFE＝∠B.
（1）求证△ADF∽△DEC；
（2）若BE＝2，AD＝6，且DF=
DE，求DF的长度．
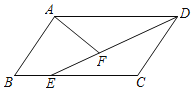
【答案】（1）见解析；（2）DF=4
【解析】
（1）根据平行四边形的性质得到∠ADF＝∠DEC，∠C+∠B=180°，根据∠AFE＝∠B得到∠AFD=∠C，根据相似三角形的判定定理即可证明；
（2）根据相似三角形的性质列出比例式，代入计算即可．
解：（1）证明：∵四边形ABCD是平行四边形，
∴∠C+∠B＝180°，∠ADF＝∠DEC，
∵∠AFD+∠AFE＝180°，∠AFE＝∠B，
∴∠AFD＝∠C，
∴△ADF∽△DEC；
（2）∵△ADF∽△DEC
∴
∵四边形ABCD是平行四边形，AD=6，BE=2
∴EC=BC-BE=AD-BE=4，
又∵DF=
DE
∴DE=
DF
∴
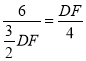
解得DF=4.
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
