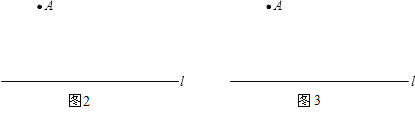题目内容
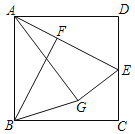
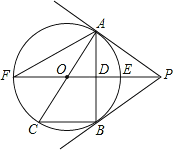
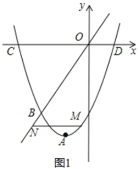
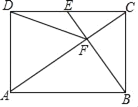
【题目】(问题探究)如图1,![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 到直线
到直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() 的距离为1,
的距离为1,![]() ,
,![]() ,则
,则![]() 的最小值是______;(提示:将线段
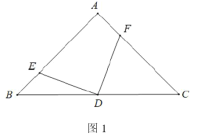
的最小值是______;(提示:将线段![]() 沿
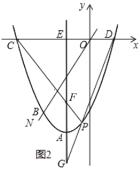
沿![]() 方向平移1个单位长度即可解决,如图2所示.)
方向平移1个单位长度即可解决,如图2所示.)
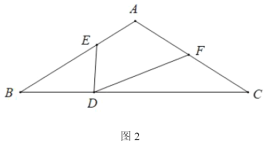
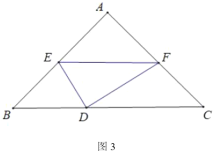
(关联运用)如图3,在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
【答案】![]()
![]()
【解析】
[问题探究]过点A作AH⊥b于H,过点B作BK⊥b于K,作BJ⊥AH交AH的延长线于J,连接MK、AB和AK,根据两点之间线段最短可得![]() =AM+MK≥AK(当且仅当A、M、K共线时,取等号),然后利用勾股定理求出AK即可;
=AM+MK≥AK(当且仅当A、M、K共线时,取等号),然后利用勾股定理求出AK即可;
[关联运用]过点F作直线l∥BA,交CA的延长线于点N,取AC的中点G,作C关于直线l的对称点M,连接MF、GF、MN,根据对称性和平行四边形的判定及性质推出CF=MF,GF=CE,根据两点之间线段最短可得![]() =GF+MF≥MG(当且仅当G、F、M共线时,取等号),然后利用勾股定理求出MG即可.
=GF+MF≥MG(当且仅当G、F、M共线时,取等号),然后利用勾股定理求出MG即可.
解:[问题探究]过点A作AH⊥b于H,过点B作BK⊥b于K,作BJ⊥AH交AH的延长线于J,连接MK、AB和AK

由图易知,四边形HJBK为矩形,MN=BK=1,MN∥BK,AH=2+1=3,AJ=2+1+1=4
∴四边形MNBK为平行四边形,HK=BJ
∴BN=MK
∴![]() =AM+MK≥AK(当且仅当A、M、K共线时,取等号)
=AM+MK≥AK(当且仅当A、M、K共线时,取等号)
在Rt△ABJ中,BJ=![]()
∴HK=3
∴AK=![]()
∴![]() ≥
≥![]()
即![]() 的最小值是
的最小值是![]() ;
;
故答案为:![]() ;
;
[关联运用]过点F作直线l∥BA,交CA的延长线于点N,取AC的中点G,作C关于直线l的对称点M,连接MF、GF、MN

由对称性可得CF=MF,CN=MN,∠CNF=∠MNF
∵在等腰![]() 和等腰
和等腰![]() 中,
中,![]()
∴∠FED=∠BAC=45°,EF=DF=2,AC=BC=4
∴EF∥AC,CG=AG=![]() AC=2=EF
AC=2=EF
∴四边形CEFG为平行四边形
∴GF=CE
∴![]() =GF+MF≥MG(当且仅当G、F、M共线时,取等号)
=GF+MF≥MG(当且仅当G、F、M共线时,取等号)
∵直线l∥BA
∴四边形EFNA为平行四边形,∠CNF=∠BAC=45°
∴AN=EF=2,∠CNF=∠MNF=45°
∴GN=AG+AN=4,MN=CN=AC+AN=6,∠MNC=∠CNF+∠MNF=90°
根据勾股定理可得MG=![]()
∴![]() ≥
≥![]()
即![]() 的最小值为
的最小值为![]() .
.
故答案为:![]() .
.