题目内容
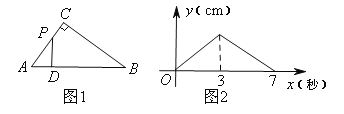
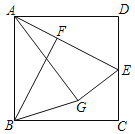
【题目】如图,在正方形ABCD中,E是CD边上一点,DE=2,过B作AE的垂线,垂足为点F,BF=3,将△ADE沿AE翻折,得到△AGE,AG与BF于点M,连接BG,则△BMG的周长为______
【答案】![]()
【解析】
延长BF交AD于K,作BH⊥AG于H.首先证明AK=DE=2,再利用相似三角形的性质求出FK,再证明∠ABK=30°,把问题特殊化后即可解决问题.
如图,延长BF交AD于K,作BH⊥AG于H.

∵四边形ABCD是正方形,
∴AB=AD,∠BAK=∠ADE=90°,
∵BF⊥AE,
∴∠AFB=90°,
∴∠BAF+∠ABF=90°,∠BAF+∠DAE=90°,
∴∠ABK=∠DAE,
∴△ABK≌△ADE(ASA),
∴AK=DE=2,
∵∠AKF=∠AKB,∠AFK=∠KAB=90°,
∴△AKF∽△BKA,
∴![]() =
=![]() ,设KF=x,
,设KF=x,
则有![]() =
=![]() ,
,
整理得![]() ,
,
解得x=1或﹣4(舍弃),
∴BK=BF+FK=3+1=4,
∵sin∠ABK=![]() =
=![]() =
=![]() ,
,
∴∠ABK=30°,
∴∠DAE=∠ABK=∠EAG=∠BAG=30°,
∴MA=MB,
在Rt△ABH中,∵AB=2![]() ,∠BAH=30°,∠AHB=90°,
,∠BAH=30°,∠AHB=90°,
∴BH=![]() AB=
AB=![]() ,AH=
,AH=![]() BH=3,
BH=3,
∵AD=AB=AG=2![]() ,
,
∴HG=2![]() ﹣3,
﹣3,
∴BG=![]() =
=![]() =3
=3![]() ﹣
﹣![]() ,
,
∴△BMG的周长=BM+GM+BG=AM+GM+BG=AG+BG=2![]() +3
+3![]() ﹣
﹣![]() .
.
故答案为:![]() .
.

【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.