Question

【题目】已知抛物线的顶点，经过点，与轴分别交于，两点．

（1）求该抛物线的解析式；

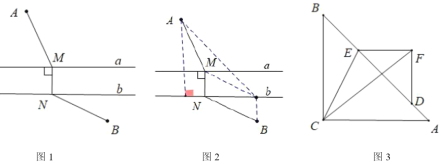
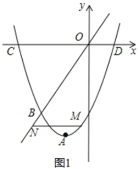
（2）如图1，点是抛物线上的一个动点，且在直线的下方，过点作轴的平行线与直线交于点，当取最大值时，求点的坐标；

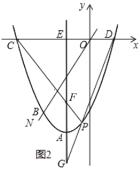
（3）如图2，轴交轴于点，点是抛物线上，之间的一个动点，直线，与分别交于，，当点运动时．

①直接写出的值；

②直接写出的值．

Answer 1

【答案】（1）；（2）（3）①8；②4

【解析】

（1）根据抛物线的顶点，设抛物线的解析式为，将点，解方程即可得到结论；

（2）设，，则的横坐标为，纵坐标为，由轴，得到根据二次函数的性质即可得到结论；

（3）过点作轴交轴于，则，，设，则，，，由根据相似三角形的判定和性质定理即可得到结论．

解：（1）∵抛物线的顶点，且经过点，

∴设抛物线的解析式为，则有：，

∴，

∴抛物线的解析式为；

（2）设直线的解析式为，

∵，

∴，

∴，

∴直线的解析式为，

设，，则的横坐标为，纵坐标为，

∵轴，

∴

∴

∴当时，的最大值为；

此时点坐标

（3）如图示，过点作轴交轴于，

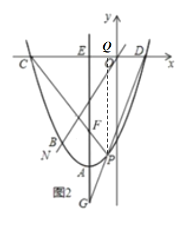
∵抛物线的解析式为；

则，，

即有，

设，则，，，

由轴可得，

则有，得，

，

由，得，

，

∴①，

，

∴②．