Question

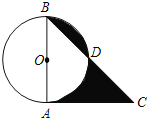
【题目】如图，在⊙O中，直径AB＝2，CA切⊙O于A，BC交⊙O于D，若∠C＝45°，则图中阴影部分的面积为（ ）

A.B.2C.πD.1

Answer 1

【答案】D

【解析】

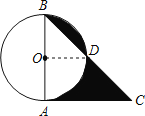
连接OD，先由直径AB＝2，CA切⊙O于A得出OB＝OA＝2，∠BAC＝90°，由∠C＝45°得出△ABC是等腰直角三角形，根据圆周角定理得出∠AOD＝90°，根据S阴影＝S△ABC﹣S△OBD﹣S扇形AOD+（S扇形BOD﹣S△OBD）进而可得出结论．

解：连接OD，

∵直径AB＝2，CA切⊙O于A，

∴OB＝OA＝2，∠BAC＝90°，

∵∠C＝45°，

∴△ABC是等腰直角三角形，

∴∠B＝45°，

∴∠AOD＝90°，

∴S阴影＝S△ABC﹣S△OBD﹣S扇形AOD+（S扇形BOD﹣S△OBD）

＝S△ABC﹣2S△OBD﹣S扇形AOD+S扇形BOD

＝S△ABC﹣2S△OBD

＝×2×2﹣2××1×1

＝2﹣1

＝1．

故选：D．