题目内容
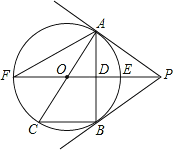
【题目】如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．
（1）求证：直线PA为⊙O的切线；
（2）试探究线段EF、OD、OP之间的等量关系，并加以证明；
（3）若BC=6，tan∠F=
，求cos∠ACB的值和线段PE的长．
【答案】（1）证明见解析（2）EF2=4ODOP，证明见解析（3）
，
【解析】解：（1）连接OB，
∵PB是⊙O的切线，∴∠PBO=90°。
∵OA=OB，BA⊥PO于D，
∴AD=BD，∠POA=∠POB。
又∵PO=PO，∴△PAO≌△PBO（SAS）。
∴∠PAO=∠PBO=90°。∴直线PA为⊙O的切线。
（2）EF2=4ODOP。证明如下：
∵∠PAO=∠PDA=90°，∴∠OAD+∠AOD=90°，∠OPA+∠AOP=90°。
∴∠OAD=∠OPA。∴△OAD∽△OPA，∴
，即OA2=ODOP。
又∵EF=2OA，∴EF2=4ODOP。
（3）∵OA=OC，AD=BD，BC=6，∴OD=
BC=3（三角形中位线定理）。
设AD=x，
∵tan∠F=
，∴FD=2x，OA=OF=2x﹣3。
在Rt△AOD中，由勾股定理，得（2x﹣3）2=x2+32，
解得，x1=4，x2=0（不合题意，舍去）。∴AD=4，OA=2x﹣3=5。
∵AC是⊙O直径，∴∠ABC=90°。
又∵AC=2OA=10，BC=6，∴cos∠ACB=
。
∵OA2=ODOP，∴3（PE+5）=25。∴PE=。
（1）连接OB，根据垂径定理的知识，得出OA=OB，∠POA=∠POB，从而证明△PAO≌△PBO，然后利用全等三角形的性质结合切线的判定定理即可得出结论。
（2）先证明△OAD∽△OPA，由相似三角形的性质得出OA与OD、OP的关系，然后将EF=2OA代入关系式即可。
（3）根据题意可确定OD是△ABC的中位线，设AD=x，然后利用三角函数的知识表示出FD、OA，在Rt△AOD中，由勾股定理解出x的值，从而能求出cos∠ACB，再由（2）可得OA2=ODOP，代入数据即可得出PE的长。
