题目内容
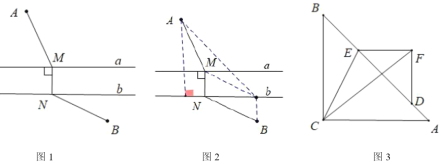
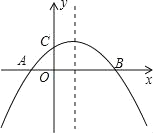
【题目】(2019·信阳一模)如图,锐角三角形ABC中,BC=6,BC边上的高为4,直线MN交边AB于点M,交AC于点N,且MN∥BC,以MN为边作正方形MNPQ,设其边长为x(x>0),正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )

A.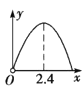 B.
B. C.
C.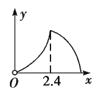 D.
D.
【答案】D
【解析】
根据题意画出符合的两种情况:分别求出函数的解析式,再判断图象即可.
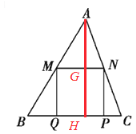
解:当PQ在边BC上时,由题意知,MN∥BC,
过A作AH⊥BC于H,交MN于G,
∴![]() ,
,
即![]() ,解得:x=2.4,
,解得:x=2.4,
当0<x≤2.4时,正方形MNQP在△ABC的内部,
∴y=x2,为开口朝上的抛物线,
当2.4<x≤4时,过A作AH⊥BC于H,交MN于G,
则![]() ,
,
即![]() ,解得:AG=
,解得:AG=![]() x,
x,
∴GH=4-![]() x,
x,
y=MN·GH=x(4-![]() x),为开口朝下的抛物线,对称轴为:x=3,
x),为开口朝下的抛物线,对称轴为:x=3,
即选项D符合题意,即答案为:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?