题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 在底边
在底边![]() 上,
上,![]() 的两边分别交
的两边分别交![]() 、
、![]() 所在直线于
所在直线于![]() 、
、![]() 两点,
两点,![]() ,
,![]() .
.
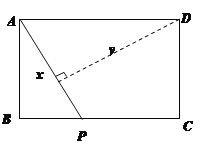
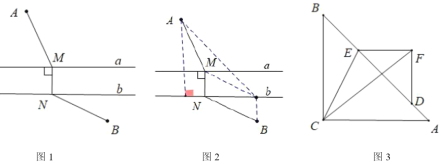
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
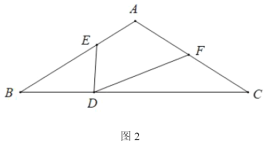
(2)如图2,求![]() 的值(含
的值(含![]() 的式子表示);
的式子表示);
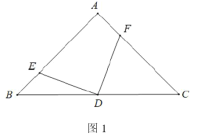
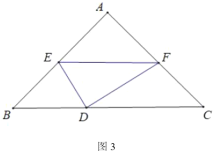
(3)如图3,连接![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,直接写出
,直接写出![]() 的值为______.
的值为______.
【答案】(1)见解析;(2)![]() ;(3)3或
;(3)3或![]()
【解析】
(1)连接![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() ,然后根据三线合一可得
,然后根据三线合一可得![]() ,从而得出
,从而得出![]() ,
,![]() ,利用ASA即可证出
,利用ASA即可证出![]() ,从而得出结论;
,从而得出结论;
(2)过点D作![]() 于
于![]() ,
,![]() 于
于![]() ,根据相似三角形的判定定理分别证出
,根据相似三角形的判定定理分别证出![]() ,
,![]() ,列出比例式即可求出结论;
,列出比例式即可求出结论;
(3)过点E作EG⊥BC于G,过点F作FH⊥BC于H,根据平行线可证△AEF∽△ABC,列出比例式可设AE=AF=5a,则AB=AC=8a,利用锐角三角函数用a表示各个线段,然后根据相似三角形的判定定理证出△GED∽△HDF,列出比例式即可列出关于n的方程,从而求出结论.
(1)证明:连接![]() ,
,
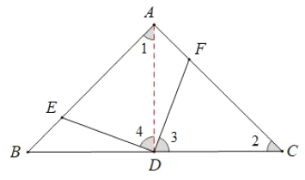
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
而![]() ,
,
![]()
![]()
![]() ;
;
(2)解:过点D作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ①
①
由(1)可知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ②
②
由①式、②式知:![]() .
.
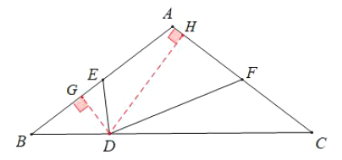
(3)过点E作EG⊥BC于G,过点F作FH⊥BC于H
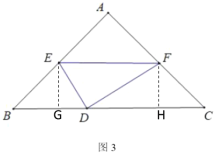
∵![]()
∴∠B=45°
∴∠B=∠C=45°,△ABC、△GBE和△HCF都为等腰直角三角形, ![]() =90°
=90°
∴GE=GB,HC=HF
∵![]() ,且
,且![]() ,
,
∴∠AEF=∠B=45°,∠AFE=∠C=45°,△AEF∽△ABC
∴AE=AF,![]()
设AE=AF=5a,则AB=AC=8a
∴BE=FC=3a
∴GE=GB=BE·cos∠B=![]() ,HF=HC=FC·cos∠C=
,HF=HC=FC·cos∠C=![]() ,BC=
,BC=![]()
∵∠EGD=∠DHF=∠EDF=90°
∴∠GED+∠EDG=90°,∠HDF+∠EDG=90°
∴∠GED=∠HDF
∴△GED∽△HDF
∴![]()
即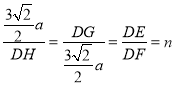
∴DH=![]() ,DG=
,DG=![]()
∵GB+DG+DH+HC=BC
∴![]() +
+![]() +
+![]() +
+![]() =
=![]()
整理,得![]()
解得:n=3或![]()
故答案为:3或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
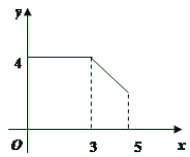
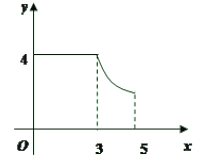
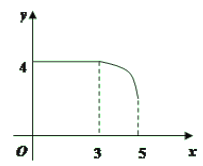
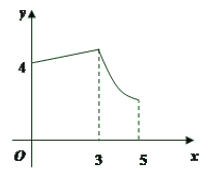
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.

【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?