题目内容
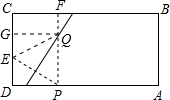
如图，矩形纸片ABCD中，AB＝5cm，BC＝10cm，E、P分别为CD、DA边上的点，ED＝2cm，PD＝3cm， PF⊥AD，折叠纸片，使P点与E点重合，折痕与PF交于Q点，则PQ的长是____________cm.
过Q点作QG⊥CD，垂足为G点，连接QE，设PQ=x，根据折叠及矩形的性质，用含x的式子表示Rt△EGQ的三边，再用勾股定理列方程求x即可．
解：过Q点作QG⊥CD，垂足为G点，连接QE，
设PQ=x，由折叠及矩形的性质可知，
EQ=PQ=x，QG=PD=3，EG=DG-DE=PQ-DE=x-2，
在Rt△EGQ中，由勾股定理得
EG2+GQ2=EQ2，即：（x-2）2+32=x2，
解得：x=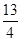
，即PQ=．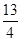
故答案为：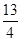
解：过Q点作QG⊥CD，垂足为G点，连接QE，
设PQ=x，由折叠及矩形的性质可知，EQ=PQ=x，QG=PD=3，EG=DG-DE=PQ-DE=x-2，
在Rt△EGQ中，由勾股定理得
EG2+GQ2=EQ2，即：（x-2）2+32=x2，
解得：x=
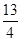，即PQ=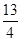．故答案为：
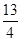
练习册系列答案
相关题目
