题目内容
(本题满分7分)如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.

(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?

(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
证明:(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
又∵DE=DE,
∴△ADE≌△CDE,
∴∠DAE=∠DCE.
(2)我判断FG=3EF.
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
∵∠DAE=∠DCE,
∴∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴EF/CE=CE/EG,
∵△ADE≌△CDE,
∴AE=CE,
∴EF/CE=CE/EG=1/2,
∵AE=2EF,
∴EG=2AE=4EF,
∴FG=EG-EF=4EF-EF=3EF
∴AD=CD,∠ADE=∠CDB;
又∵DE=DE,
∴△ADE≌△CDE,
∴∠DAE=∠DCE.
(2)我判断FG=3EF.
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
∵∠DAE=∠DCE,
∴∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴EF/CE=CE/EG,
∵△ADE≌△CDE,
∴AE=CE,
∴EF/CE=CE/EG=1/2,
∵AE=2EF,
∴EG=2AE=4EF,
∴FG=EG-EF=4EF-EF=3EF
略

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?
 中,AE是BC边上的高,将
中,AE是BC边上的高,将 沿
沿 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得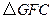 .
.
 ;
; ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论. 的边长是4cm,点
的边长是4cm,点 在边
在边 上,以
上,以 为边向外作正方形
为边向外作正方形 ,连结
,连结 、
、 、
、 ,则
,则 的面积是_____________cm2.
的面积是_____________cm2.



 中,
中, 为锐角,点
为锐角,点 为射线
为射线 上一点,联结
上一点,联结 ,以
,以 .
. ,
, ,
, 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段


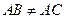 ,
, 是锐角,点
是锐角,点 满足什么条件时,
满足什么条件时, (点
(点 不重合),并说明理由.
不重合),并说明理由.