Question

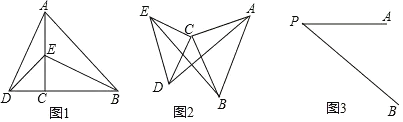
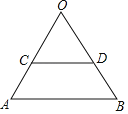
【题目】如图，△ABO是正三角形，CD∥AB，把△ABO绕△OCD的内心P旋转180°得到△EFG

（1）在图中画出点P和△EFG，保留画图痕迹，简要说明理由

（2）若AO＝3，CD＝2，求A点运动到E点路径的长．

Answer 1

【答案】（1）详见解析；（2）π．

【解析】

（1）根据正三角形的三线合一的性质，先画出△OCD的角平分线的交点，即为点P，再把△ABO绕着△OCD的内心P旋转180°得到△EFG即可；

（2）先根据等边三角形的性质求出OH和△OCD的高，进而求得额OP、PH的长，再根据勾股定理求得PA的长，由于点A运动到点D的运动路线是半圆，进而由弧长公式或圆的周长来求得答案即可．

解：（1）点P和△EFG如图所示．

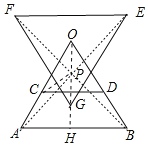
（2）延长OP交CD于G，交AB于H，

∵OA＝3，CD＝2，

∴OP＝2，OH＝，

∴PH＝OH﹣OP＝，AH＝HB＝，

∴

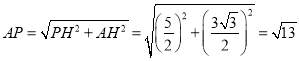
∴A点运动到E点路径的长＝．