Question

【题目】（1）问题发现

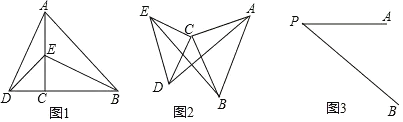
如图1，△ACB和△DCE均为等腰直角三角形，∠ACB=90°，B，C，D在一条直线上，填空：线段AD，BE之间的关系为

（2）拓展探究

如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，请判断AD，BE的关系，并说明理由．

（3）解决问题

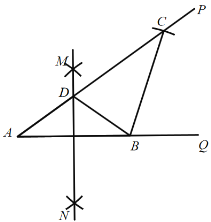
如图3，线段PA=，点B是线段PA外一点，PB=3，连接AB绕点A逆时针旋转90°得到线段AC，随着点B的位置变化，直接写出PC的范围．

Answer 1

【答案】（1）AD=BE，AD⊥BE；（2）AD=BE，AD⊥BE，理由见解析；（3）1≤PC≤5.

【解析】

（1）可先证明△ACE≌△BCD，再根据全等三角形的对应边相等可证得AE=BD，延长BD交AE于点F，由△ACE≌△BCD，再结合条件可得到∠ADF+∠FAD=90°，可得到AE⊥BD；

（2）仿照（1）先证明△ACE≌△BCD，可得AE=BD，再转换得到∠BOH+∠OBH=90°，可得到AE⊥BD；

（3）如图3中，作AE⊥AP，使得AE=PA，则易证△APE≌△ACP，可得PC=BE，求出BE的范围即可解决问题.

解：（1）结论：AD=BE，AD⊥BE，

理由：如图1中，

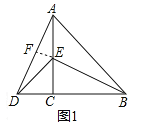
∵△ACB与△DCE均为等腰直角三角形，

∴AC=BC，CE=CD，

∠ACB=∠ACD=90°，

在△ACD和△BCE中

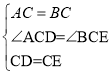
∴△ACD≌△BCE（SAS），

∴AD=BE，∠EBC=∠CAD，

延长BE交AD于点F，

∵BC⊥AD，

∴∠EBC+∠CEB=90°，

∵∠CEB=AEF，

∴∠EAD+∠AEF=90°，

∴∠AFE=90°，即AD⊥BE，

∴AD=BE，AD⊥BE，

故答案为AD=BE，AD⊥BE；

（2）结论：AD=BE，AD⊥BE，

理由：如图2中，设AD交BE于H，AD交BC于O，

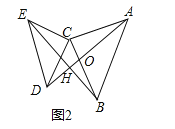
∵△ACB与△DCE均为等腰直角三角形，

∴AC=BC，CE=CD，∠ACB=∠ECD=90°，

∴ACD=∠BCE，

在△ACD和△BCE中

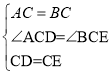
∴△ACD≌△BCE（SAS），

∴AD=BE，∠CAD=∠CBE，

∵∠CAO+∠AOC=90°，∠AOC=∠BOH，

∴∠BOH+∠OBH=90°，

∴∠OHB=90°，

∴AD⊥BE，

∴AD=BE，AD⊥BE；

（3）如图3中，作AE⊥AP，使得AE=PA，

∴∠EAP=90°，

∵连接AB绕点A逆时针旋转90°得到线段AC，

∴AB=AC，∠BAC=90°，

∴∠EAP+∠PAB=∠BAC+∠PAB，

∴∠EAB=∠PAC，

在△EAB和△PAC中

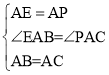
∴△EAB≌△PAC（SAS），

∴PC=BE，

∵PA=，

在等腰直角△PAE中，

PE=，

图3-1中，当P、E、B共线时，BE最小，最小值=PB-PE=1，

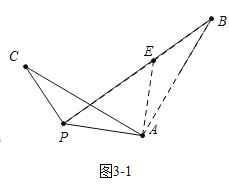
图3-2中，当P、E、B共线时，BE最大，最大值=PB+PE=5，

∴1≤BE≤5，即1≤PC≤5.