Question

【题目】在中，，，以为边在的另一侧作，点为射线上任意一点，在射线上截取，连接、、．

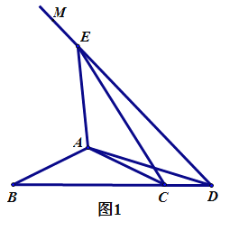
（1）如图1，当点落在线段的延长线上时，的度数为__________．

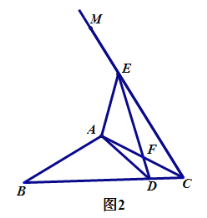
（2）如图2，当点落在线段（不含边界）上时，与交于点，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；

（3）在（2）的条件下，若，求的最大值．

Answer 1

【答案】（1）；（2）见解析；（3）的最大值为9

【解析】

（1）通过证△ABD≌△ACE，来求∠ADE的角度

（2）如下图，先证，到得∠1=∠2，在推导出∠DAE的角度，进而得出结论；

（3）利用得到AF、AD、AC之间的关系，当最短时，最短、最长，从而求得CF的长

（1）∵AB=AC，∠BAC=120°

∴∠B=∠ACB=30°

∵∠ACM=∠ACB

∴∠B=∠ACM

又∵BD=CE

∴ABD≌ACE

∴AD=AE，∠EAD=120°

∴∠ADE=30°

（2）（1）中的结论还成立

证明：（如图所示）．

∵，，

∴．

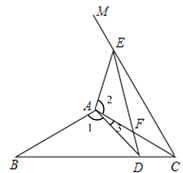
又∵，∴．

又∵，∴．

∴，．

∴．即．

又∵，∴．

（3）∵，，∴．

∵且，

∴．∴．∴．

∴．∴

∴当最短时，最短、最长．

易得当时，最短、最长，此时．

∴的最大值为9