Question

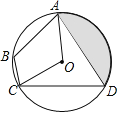
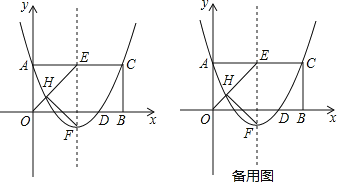
【题目】如图，在正方形中，点在边上运动（不运动至两端点），射线，交于点，为的外接圆，连结，，．

（1）求的度数．

（2）求证：．

（3）若正方形的边长为．

①当为中点时，求四边形的面积．

②设，交于点，设，，的面积分别为，，，当平分时，_________（直接写出答案）．

Answer 1

【答案】（1）45°；（2）见解析；（3）①3，②

【解析】

（1）根据正方形的性质和弧的度数等于弧所对的圆心角的度数，即可求出．

（2）可证得△OAB≌△OAD，求出∠OAD度数，∠OFB=45°，在四边形OADF中，利用四边形内角和，即可证得．

（3）①四边形OAEF的面积=△OAD的面积+△ODF的面积-△FDE的面积，作OH⊥AD，OG⊥FD，垂足分别为H，G，连结OD，分别求得△OAD的面积、△ODF的面积和△FDE的面积，即可求解．

②可证得∴所以，，，的面积分别为，，，它们的高均为MD，为求面积比，即可求来，设圆的半径为r，可将BE、ME、MF均用r表示出来即可求解．

（1） 解：∵∠ADB=45°， ∠ADF=90°，

∴∠BDF=135°

∴优弧=270°．

∴=90°，∠BOF =90°

∵OB=OF，

∴∠OFB=∠OBF=45°

故答案为：45°

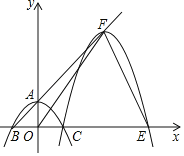
（2）证明：连结OD（如图１），

∵OB=OD，OA=OA，AB=AD，

∴△OAB≌△OAD（SSS）．

∴∠OAB=∠OAD=．

∵∠OFB=45°，

∴∠AOF+∠AEF=360°-135°-45°=180°

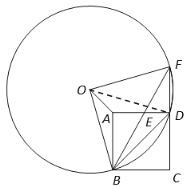
图1

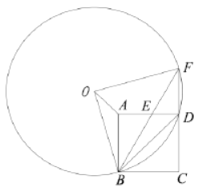
（3）①作OH⊥AD，OG⊥FD，垂足分别为H，G，连结OD（如图2），

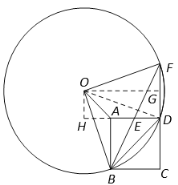
图2

由AE=ED，易得△ABE≌△DFE，

∴FD=AB=2，

由OD=OF，OG⊥FD，得GD=

由OH⊥AD，OG⊥FD，∠ADF=90°，得矩形OHDG，

∴OH=GD=1．

由∠OAH=∠OAB-∠HAB=135°-90°=45°，

得∠HOA=∠HAO=45°

∴AH=OH=1，OG=HD=AH+AD=1+2=3．

∵△OAD的面积=，

△ODF的面积=，

△FDE的面积=，

∴四边形OAEF的面积=△OAD的面积+△ODF的面积-△FDE的面积=1+3-1=3．

②OD与BF交于点M如图3：

平分

∴

又∵

∴

∴

∵OF=OB

∴BM=MF

设圆的半径为r

BM=MF=

∵

∵

∴

∴

，

，，的面积分别为，，，三个三角形的高均为MD

∴

图3

故答案为：