Question

【题目】如图，已知二次函数：和二次函数：图象的顶点分别为、，与轴分别相交于、两点（点在点的左边）和、两点（点在点的左边），

　　　　　

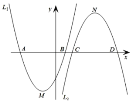
（1）函数的顶点坐标为______；当二次函数，的值同时随着的增大而增大时，则的取值范围是_______；

（2）判断四边形的形状（直接写出，不必证明）；

（3）抛物线，均会分别经过某些定点；

①求所有定点的坐标；

②若抛物线位置固定不变，通过平移抛物线的位置使这些定点组成的图形为菱形，则抛物线应平移的距离是多少？

Answer 1

【答案】（1），；（2）四边形是矩形；（3）①所有定点的坐标，经过定点或，经过定点或；②抛物线应平移的距离是或．

【解析】

（1）将已知抛物线解析式转化为顶点式，直接得到点M的坐标；结合函数图象填空；
（2）利用抛物线解析式与一元二次方程的关系求得点A、D、M、N的横坐标，可得AD的中点为（1，0），MN的中点为（1，0），则AD与MN互相平分，可证四边形AMDN是矩形；
（3）①分别将二次函数的表达式变形为和，通过表达式即可得出所过定点；

②根据菱形的性质可得EH1=EF=4即可，设平移的距离为x，根据平移后图形为菱形，由勾股定理可得方程即可求解．

解：（1），顶点坐标为，

由图象得：当时，二次函数，的值同时随着的增大而增大．

故答案为：；；

（2）结论：四边形是矩形．

由二次函数和二次函数解析式可得：

点坐标为，，点坐标为，，

顶点坐标为，顶点坐标为，

的中点为，的中点为，

与互相平分，

四边形是平行四边形，

又，

∴□是矩形；

（3）①二次函数，

故当或时，即二次函数经过、两点，

二次函数，

故当或时，即二次函数经过、两点，

②二次函数经过、两点，二次函数经过、两点，

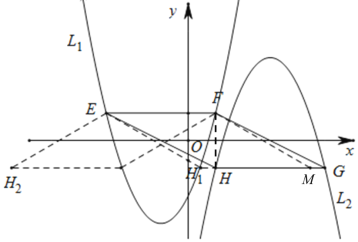
如图：四个定点分别为、，、，则组成四边形为平行四边形，

∴FH⊥HG，FH=2，HM=4-x，

设平移的距离为，根据平移后图形为菱形，

则EH1=EF=H1M=4，

由勾股定理可得：FH2+HM2=FM2，

即，

解得：，

抛物线位置固定不变，通过左右平移抛物线的位置使这些定点组成的图形为菱形，则抛物线应平移的距离是或．