题目内容
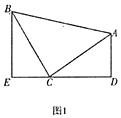
【题目】我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。
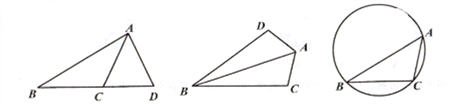
(1)如图1,已知AD=AC,请写出图中的友好三角形;
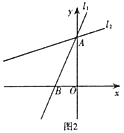
(2)如图2,在△ABC和△ABD中,AD=AC,∠BDA=∠BCA,且∠BDA>90°,
求证:△ABC≌△ABD;
(3) 如图3,△ABC内接于圆,∠ABC=30°,∠BAC=45°,BC=4。D是圆上一点,若△ABD和△ABC是友好三角形,且BD<AD,求AD的长。
【答案】(1)△ABC和△ABD (2)见解析 (3)![]()
【解析】(1)根据友好三角形的概念判断即可;(2)连结CD,由等腰三角形的性质得出∠ADC=∠ACD,再由∠ADB=∠ACB,根据等量代换推出∠BDC=∠BCD,继而得出BD=CD,利用SSS即可得证;(3)分三种情况讨论:① 当AB=AB,AD=BC时;② 当AB=AB,DB=AC时;③ 当AB=AB,BD=BC时去分析求解.
(1):如图, △ABC和△ABD
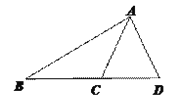
(2):连结CD,
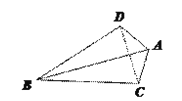
∵AD=AC, ∴∠ADC=∠ACD
∵∠ADB=∠ACB,
∴![]() ,即
,即![]()
∴BD=CD
∵AB=AB, ∴ △ABC≌△ABD (SSS)
(3)① 如图,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形. ∴AD =4
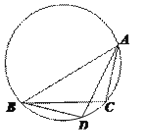
② 如图,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形.
过C作CE⊥AB于点E
∵![]() ,BC=4, ∴
,BC=4, ∴ ![]()
∵![]() , ∴
, ∴![]()
∴![]()
∵![]() , ∴
, ∴![]()
∴![]() ,即
,即![]()
∴![]()

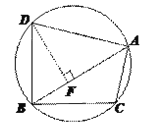
③ 如图9,当![]() 时,
时,![]() ,
,
△ABD和△ABC是友好三角形.
过D作DF⊥BA于点F
∵![]() ∴
∴![]() ,
,![]()
∴![]() , ∴
, ∴![]()
∴![]()
综上所述:AD的长度为![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目