Question

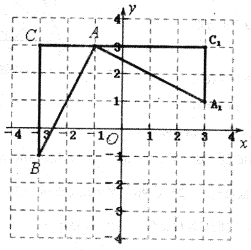
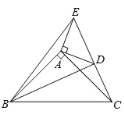
【题目】如图1，等腰直角三角形中，，，直线经过点，过作于，过作于.

（1）求证：.

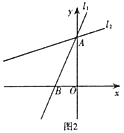
（2）已知直线与轴交于点，将直线绕着点顺时针旋转45°至，如图2，求的函数解析式.

Answer 1

【答案】（1）见解析；（2）y=x+4；

【解析】

（1）先根据△ABC为等腰直角三角形得出CB=CA，再由AAS定理可知；

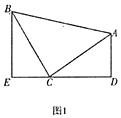
（2）过点B作BC⊥AB于点B，交l2于点C，过C作CD⊥x轴于D，根据∠BAC=45°可知△ABC为等腰Rt△，由（1）可知△CBD≌△BAO，由全等三角形的性质得出C点坐标，利用待定系数法求出直线l2的函数解析式即可；

(1)证明：∵△ABC为等腰直角三角形，

∴CB=CA，

又∵AD⊥CD，BE⊥EC，

∴∠D=∠E=90°,∠ACD+∠BCE=180°90°=90°，

又∵∠EBC+∠BCE=90°，

∴∠ACD=∠EBC，

在△ACD与△CBE中，

，

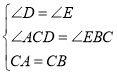∴ (AAS)；

(2)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,

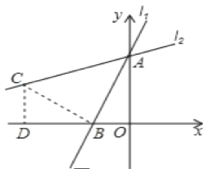
∵∠BAC=45°，

∴△ABC为等腰Rt△，

由(1)可知：△CBD≌△BAO，

∴BD=AO，CD=OB，

∵直线l1:y=x+4，

∴A(0,4),B(3,0)，

∴BD=AO=4.CD=OB=3，

∴OD=4+3=7，

∴C(7,3),

设l2的解析式为y=kx+b(k≠0)，

∴ ，

∴ ，

∴l2的解析式：y=x+4；