题目内容
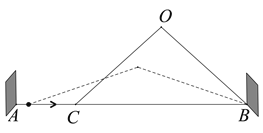
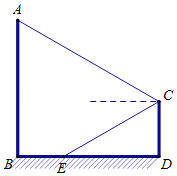
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
【答案】立柱CD的高为(15﹣![]() )米.
)米.
【解析】作CH⊥AB于H,得到 BD=CH,设CD=x米,根据正切的定义分别用x表示出HC、ED,根据正切的定义列出方程,解方程即可.
作CH⊥AB于H,
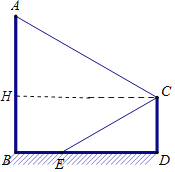
则四边形HBDC为矩形,
∴BD=CH,
由题意得,∠ACH=30°,∠CED=30°,
设CD=x米,则AH=(30-x)米,
在Rt△AHC中,HC=![]() ,
,
则BD=CH=![]() (30-x),
(30-x),
∴ED=![]() (30-x)-10,
(30-x)-10,
在Rt△CDE中,![]() =tan∠CED,即
=tan∠CED,即![]() ,
,
解得,x=15-![]() ,
,
答:立柱CD的高为(15-![]() )米.
)米.

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】借助表格进行多项式乘多项式运算,可以方便合并同类项得出结果.下面尝试利用表格试一试.
例题:(a+b)(a﹣b)
解填表
| a | b |
a | a2 | ab |
﹣b | ﹣ab | ﹣b2 |
则(a+b)(a﹣b)=a2﹣b2.
根据所学完成下列问题.
(1)如表,填表计算(x+2)(x2﹣2x+4),(m+3)(m2﹣3m+9),直接写出结果.
| x2 | ﹣2x | 4 |
x | x3 | ﹣2x2 | 4x |
+2 | 2x2 | ﹣4x | 8 |
| m2 | ﹣3m | 9 |
m | m3 | ﹣3m2 | 9m |
+3 | 3m2 | ﹣9m | 27 |
结果为 ;结果为 .
(2)根据以上获得的经验填表:
| |||
△ | △3 | ||
〇 | 〇3 |
结果为△3+〇3,根据以上探索,请用字母a、b来表示发现的公式为 .
(3)用公式计算:(2x+3y)(4x2﹣6xy+9y2)= ;
因式分解:27m3﹣8n3= .
【题目】小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
次数x | 1 | 2 | 3 | 4 | … |
余额y | 100-1.2 | 100-2.4 | 100-3.6 | 100-4.8 | … |
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?