Question

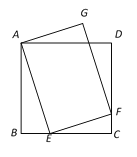
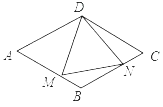
【题目】如图，在边长为4的菱形ABCD中，∠A＝60°，点M、N是边AB、BC上的动点，若△DMN为等边三角形，点M、N不与点A、B、C重合，则△BMN面积的最大值是_____．

Answer 1

【答案】

【解析】

先判断出△DMB≌△DNC，进而判断出当△DMN的面积最小时，△BMN的面积最大，即可得出结论．

解：连接BD，

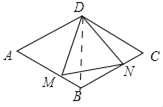
∵四边形ABCD是菱形，

∴BD＝CD，DN＝DM，

∵∠BDM＝∠MDN﹣∠BDN，

∵∠CDN＝∠BDC﹣∠BDN，∠MDN＝∠BDC＝60°，

∴∠CDN＝∠BDM，

∴△DMB≌△DNC（SAS），

∴S△DMB＝S△DNC，

∴S四边形DMBN＝S△DBC,

∵S△BMN＝S四边形DMBN﹣S△DMN，

∴当△DMN的面积最小时，△BMN的面积最大，

当DN⊥BC时，△DMN的边长最短，

即：△DMN的面积最小，此时DN＝，

即：S△DMN＝，

∴△BMN的面积的最大值为,

故答案为：.