Question

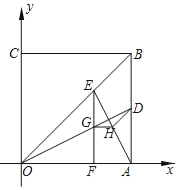
【题目】已知抛物线y1＝ax2+b经过C（﹣2，4），D（﹣4，4）两点．

（1）求抛物线y1的函数表达式；

（2）将抛物线y1沿x轴翻折，再向右平移，得到抛物线y2，与y2轴交于点F，点E为抛物线2上一点，要使以CD为边，C、D、E、F四点为顶点的四边形为平行四边形，求所有满足条件的抛物线y2的函表达式．

Answer 1

【答案】（1）y＝﹣x2﹣3x；（2）y2＝（x+1）2﹣或y2＝（x﹣1）2﹣．

【解析】

（1）将点C、D坐标代入抛物线表达式，即可求解；

（2）变换后抛物线的表达式为：y2＝（x+3﹣m）2﹣，C、D、E、F四点为顶点的四边形为平行四边形，则点F（0，﹣4），将点F坐标代入y2表达式，即可求解．

解：（1）将点C、D坐标代入抛物线表达式得：，解得：，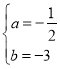

故抛物线y1的函数表达式为：y＝﹣x2﹣3x；

（2）将抛物线y1沿x轴翻折的表达式为：y＝（x+3）2﹣，

设再向右平移m个单位得：y2＝（x+3﹣m）2﹣，

C、D、E、F四点为顶点的四边形为平行四边形，

C（﹣2，4），D（﹣4，4），则CD∥x轴，

则点F（0，﹣4），

将点F坐标代入y2表达式得：﹣4＝（0+3﹣m）2﹣，

解得：m＝2或4，

故：y2＝（x+1）2﹣或y2＝（x﹣1）2﹣．