题目内容
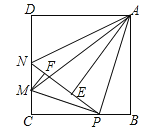
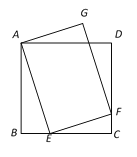
【题目】如图,已知正方形ABCD中,点E是BC上的一个动点,EF⊥AE交CD于点F,以AE,EF为边作矩形AEFG,若AB=4,则点G到AD距离的最大值是________.
【答案】![]()
【解析】
因∠AEF=90°得∠AEB+∠FEC=90°,在Rt△ABE中∠BAE+∠CEF=90°,根据同角的余角相等得∠BAE=∠FEC,可证明△ABE∽△ECF;由相似三角形的性质和二次函数可求点G到AD距离的最大值是1.
解:设BE=x,FC=y,
∵EF⊥AE,
∴∠AEB+∠FEC=90°,
又∵四边形ABCD是正方形,
∴∠B=∠C=90°
∴∠BAE+∠AEB=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF(AA),
∴![]() ,
,
即![]() ,
,
![]() ,
,
∵点G到AD距离就是FC的长度,
∴点G到AD距离的最大值是1,
故答案为1.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目