题目内容
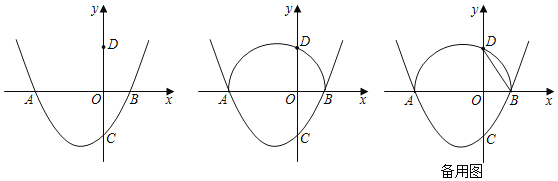
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
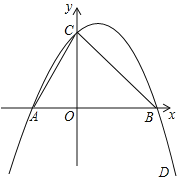
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
【答案】(1)y=-x2+2x+3;(2)6;(3)点P有4个,分别是(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ),(
),(![]() ,﹣
,﹣![]() )
)
【解析】
试题分析:(1)用待定系数法:设二次函数的解析式为y=ax2+bx+c(a≠0) ,由题意可得抛物线经过B,C,D三点,将这三点坐标代入抛物线解析式,求出a,b,c,的值即可求出抛物线的解析式;(2)由解析式求出A,点坐标,再由B,C点坐标求出AB,OC的值,利用三角形面积公式求出△ABC的面积;(3)由上题可知S△ABP=6÷2=3,设P点的纵坐标为n,因为AB是4,所以由面积求出三角形ABP的高,即n的绝对值,再分别带入抛物线解析式,即可求出P点横坐标,对应写出P点坐标即可.
试题解析:(1)设二次函数的解析式为y=ax2+bx+c(a≠0) ,由题意可得函数经过B(3,0),C(0,3),D(4,-5)三点,将三点坐标代入得: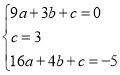 ,解得a=-1,b=2,c=3,所以二次函数的解析式为y=-x2+2x+3;(2)由题意得,当y=0时,-x2+2x+3=0 ,解得:x1=-1,x2=3 ,∴A点坐标为(-1,0),∵B(3,0),C(0,3),∴AB=4,OC=3,∴S△ABC= 4×3÷2=6,即△ABC的面积是6;(3)设P点的纵坐标为n,∵S△ABP=
,解得a=-1,b=2,c=3,所以二次函数的解析式为y=-x2+2x+3;(2)由题意得,当y=0时,-x2+2x+3=0 ,解得:x1=-1,x2=3 ,∴A点坐标为(-1,0),∵B(3,0),C(0,3),∴AB=4,OC=3,∴S△ABC= 4×3÷2=6,即△ABC的面积是6;(3)设P点的纵坐标为n,∵S△ABP=![]() S△ABC,∴S△ABP=3,即
S△ABC,∴S△ABP=3,即![]() AB|n|=3,AB=4,代入解得n=±
AB|n|=3,AB=4,代入解得n=±![]() ,∴
,∴![]() =﹣x2+2x+3,解得:x=
=﹣x2+2x+3,解得:x=![]() 或-
或-![]() =﹣x2+2x+3,解得:x=
=﹣x2+2x+3,解得:x=![]() ,∴这样的点P有4个,它们分别是(
,∴这样的点P有4个,它们分别是(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ),(
),(![]() ,﹣
,﹣![]() )
)