题目内容
【题目】某公司从年初以来累计利润S（万元）与时间t（月）之间的关系（即前t个月的利润总和S和t之间的关系）为二次函数关系．试根据图象提供的信息，解答下列问题：
（1）求累计利润S（万元）与时间t（月）之间的函数表达式；
（2）截至几月末该公司累计利润可达16万元？
（3）第10个月该公司所获利润是多少万元？
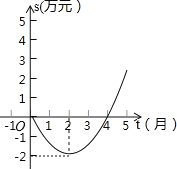
【答案】（1）S＝
t2﹣2t；（2）8；（3）7.5万元
【解析】
（1）根据图象利用待定系数法求解即可；
（2）把S＝16代入（1）中函数关系式，求得月份即可；
（3）分别把t＝9，t＝10，代入函数解析S＝t2﹣2t，再把总利润相减即可得出．
解：（1）由图象可知其顶点坐标为（2，﹣2），
故可设其函数关系式为：S＝a（t﹣2）2﹣2．
∵所求函数关系式的图象过（0，0），
于是得：a（0﹣2）2﹣2＝0，
解得a＝．
∴所求函数关系式为：S＝（t﹣2）2﹣2，即S＝t2﹣2t．
（2）把S＝16代入S＝（t﹣2）2﹣2，
得 （t﹣2）2﹣2＝16，
解得t1＝8，t2＝﹣4（舍去），
答：截止到8月末公司累积利润可达16万元；
（3）把t＝9代入关系式，得S＝×92﹣2×9＝22.5，
把t＝10代入关系式，得S＝×102﹣2×10＝30，
30﹣22.5＝7.5，
答：第10个月公司所获利润是7.5万元．
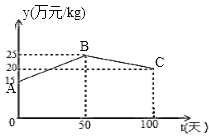
【题目】经过市场调查得知，某种商品的销售期为100天，设该商品销量单价为y(万元/kg)，y与时间t(天)函数关系如下图所示，其中线段AB表示前50天销售单价y(万元/kg)与时间t(天)的函数关系；线段BC的函数关系式为y=-
t+m.该商品在销售期内的销量如下表：
时间t(天) | 0＜t≤50 | 50＜t≤100 |
销量(kg) | 200 |
|
(1)分别求出当0＜t≤50和50＜t≤100时y与t的函数关系式；
(2)设每天的销售收入为w(万元)，则当t为何值时，w的值最大？求出最大值；
