Question

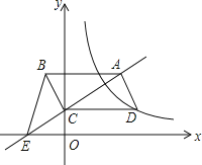
【题目】如图，平行四边形ABCD的顶点C在y轴正半轴上，CD平行于x轴，直线AC交x轴于点E，BC⊥AC，连接BE，反比例函数 (x＞0)的图象经过点D．已知S△BCE=1，则k=______．

Answer 1

【答案】2

【解析】

设D点坐标为(m，n)，则AB=CD=m，由平行四边形的性质可得出∠BAC=∠CEO，结合∠BCA=∠COE=90°，即可证出△ABC∽△ECO，根据相似三角形的性质可得出BCEC=ABCO=mn，再根据S△BCE=1，即可求出k=2，此题得解．

解：设D点坐标为(m，n)，则AB=CD=m，

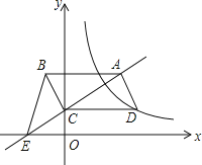
∵CD平行于x轴，AB//CD，

∴∠BAC=∠CEO．

∵BC⊥AC，∠COE=90°，

∴∠BCA=∠COE=90°，

∴△ABC∽△ECO，

∴，

∴∴BCEC=ABCO=mn．

∵反比例函数y=(x＞0)的图象经过点D，

∴k=mn=BCEC=2S△BCE=2．

故答案为：2．