��Ŀ����
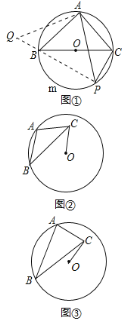
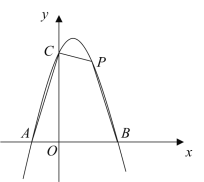
����Ŀ����ͼ��������y=-![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����B����Ϊ(4��0)����C����Ϊ(0��4)����D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����B����Ϊ(4��0)����C����Ϊ(0��4)����D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
��1���������ߵı���ʽ���Գ��
��2����F���������ϵĶ��㣬����FBA��2��BDEʱ�����F�����ꣻ
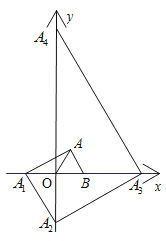
��3������P��x���Ϸ��������ϵĶ��㣬��PBΪ����������PBGH�����ŵ�P���˶��������εĴ�С��λ��Ҳ���Ÿı䣬������G��Hǡ������y����ʱ����ֱ��д����P�ĺ����꣮
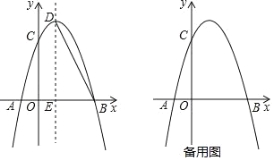
���𰸡���1��![]() ��x=1����2��(
��x=1����2��(![]() ��
��![]() )��(
)��(![]() ��-
��-![]() )����3����P�ĺ�����Ϊ
)����3����P�ĺ�����Ϊ![]() ��0��2��2-
��0��2��2-![]()
��������
��1������B��C��������������߱���ʽ��������⣻
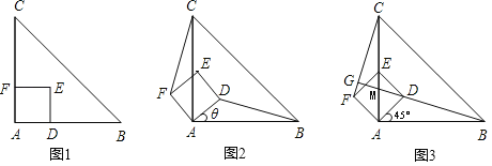
��2�����߶�DE��ȡ��M��ʹMD=MB����ʱ��EMB=2��BDE�����FBA=��EMB��������⣻
��3���ֵ�P�ڶԳ����Ҳࡢ��P�ڶԳ�������������������������ȫ����⼴�ɣ�
��1�����������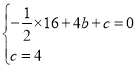
![]()
��![]()
![]()
��D�����꣨1��![]() �����Գ���Ϊx=1
�����Գ���Ϊx=1
��2����ͼ�����߶�DE��ѡȡ��M��ʹ��MD=MB����ʱ��EMB��2��BDE
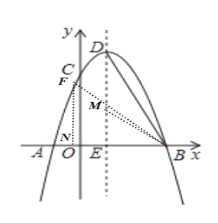
��ME=a����Rt��BME��ME2BE2BM2.
��![]() �����a��
�����a��![]()
��tan��EMB=![]()
��F��FN��x���ڵ�N����F��m����![]() m2+m+4������FN��|��
m2+m+4������FN��|��![]() m2+m+4|
m2+m+4|
�ߡ�FBA��2��BDE��
���FBA����EMB��
��tan��FBA=tan��EMB=![]()
��B��4��0����E��1��0����
��BE��3��BN��4/span>��m����tan��FBA=
����F��x���Ϸ�ʱ����12(4��m)��5����![]() m2+m+4�������m1��4(��)��m2��
m2+m+4�������m1��4(��)��m2��![]()
��F�����꣨![]() ��
��![]() ��
��
����F��x���·�ʱ����-12(4��m)��5����![]() m2+m+4�������m1��4(��)��m2��
m2+m+4�������m1��4(��)��m2��![]() ��F�����꣨
��F�����꣨![]() ��-
��-![]() ��
��
��F�����꣨![]() ��
��![]() ����
����![]() ��-
��-![]() ��
��
��3�����ٵ���P�ڶԳ����Ҳ�ʱ��
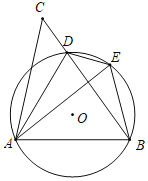
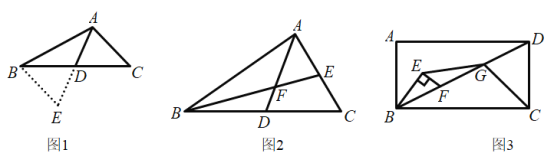
����������H��y����ʱ����ͼ2��
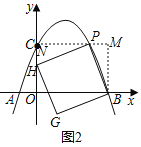
�ߡ�MPB+��CPH=90������CPH+��CHP=90����
���CHP=��MPB��
�ߡ�BMP=��PNH=90����PH=BP��
���BMP�ա�PNH��AAS����
��MB=PC��
���P��x��y������x=y=-![]() x2+x+4��
x2+x+4��
��ã�x=��2![]() ����ȥ��ֵ����
����ȥ��ֵ����
�ʵ�P�ĺ�����Ϊ2![]() ��
��
����������G��y����ʱ����ͼ3��
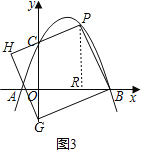
����P��PR��x���ڵ�R��
ͬ���ɵã���PRB�ա�BOG��AAS����
��PR=OB=4��
��yP=4=-![]() x2+x+4��
x2+x+4��
��ã�x=2��
�ڵ���P�ڶԳ������ʱ��
ͬ���ɵã���P�ĺ�����Ϊ0��2-2![]() ��
��
���ϣ���P�ĺ�����Ϊ![]() ��0��2��2-
��0��2��2-![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�