题目内容
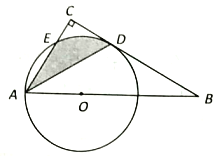
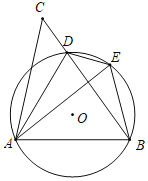
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)求证:AE=AB.
(2)填空:
①当∠CAB=90°,cos∠ADB=![]() ,BE=2时,边BC的长为 .
,BE=2时,边BC的长为 .
②当∠BAE= 时,四边形AOED是菱形.
【答案】(1)见解析;(2)①3![]() ;②60°
;②60°
【解析】
(1)利用折叠的性质得出AC=AE,∠C=∠AED,再判断出∠C=∠ABC,得出AB=AC,即可得出结论;
(2)①先求出EF=1,再判断出∠AEB=∠ADB,利用锐角三角函数求出AE,进而求出AB,即可得出结论;
②先判断出△AOD是等边三角形,得出∠ADO=60°,进而求出∠ADE=120°,再求出∠C=∠ABC=∠DAC=30°,即可求出∠BAC=120°,利用折叠的性质求出∠CAE=60°,即可得出结论.
(1)证明:由折叠知,AC=AE,∠C=∠AED,
∵∠ABC=∠AED,
∴∠C=∠ABC,
∴AB=AC,
∴AE=AB;
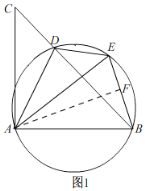
(2)①如图1,过点A作AF⊥BE于F,
由(1)知,AE=AB,
∴EF=![]() BE=1,
BE=1,
∵∠ADB=∠AEB,cos∠ADB=![]() ,
,
∴cos∠AEB=![]() ,
,
在Rt△AFE中,cos∠AEB=![]() =
=![]() ,
,
∴AE=3EF=3,
由(1)知,AE=AB,
∴AB=3,
由(1)知,AB=AC,
∵∠CAB=90°,
∴BC=![]() AB=3
AB=3![]() ,
,
故答案为3![]() ;
;
②如图2,
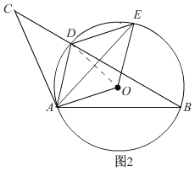
∵四边形AOED是菱形,
∴DE=OA=AD,
连接OD,
∴OA=OD,
∴AD=OA=OD,
∴△AOD是等边三角形,
∴∠ADO=60°,
同理:∠ODE=60°,
∴∠ADE=∠ADO+∠ODE=120°,
由折叠知,CD=DE,∠ADC=∠ADE,
∴∠ADC=120°,
∵AD=DE,
∴CD=AD,
∴∠DAC=∠C=![]() (180°﹣∠ADC)=30°,
(180°﹣∠ADC)=30°,
由(1)知,∠ABC=∠C,
∴∠BAC=180°﹣∠C﹣∠ABC=120°,
由折叠知,∠DAE=∠DAC=30°,
∴∠CAE=∠DAC+∠DAE=60°,
∴∠BAE=∠BAC﹣∠CAE=60°,
故答案为60°.

【题目】某公司准备购进一批产品进行销售,该产品的进货单价为6元/个.根据市场调查,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于日销售量y(个)与销售单价x(元/个)的几组数据如表:
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
(1)求出y与x之间的函数关系式(不要求写出自变量的取值范围)及m的值.
(2)按照(1)中的销售规律,当销售单价定为17.5元/个时,日销售量为 个,此时,获得日销售利润是 .
(3)为防范风险,该公司将日进货成本控制在900(含900元)以内,按照(1)中的销售规律,要使日销售利润最大,则销售单价应定为多少?并求出此时的最大利润.