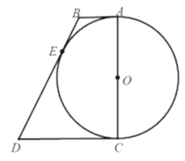
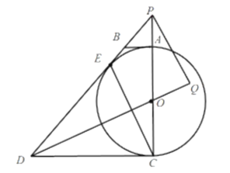
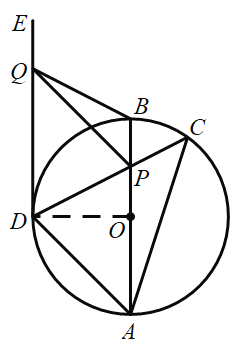
题目内容
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 右侧半圆上的一个动点,点
右侧半圆上的一个动点,点![]() 是
是![]() 左侧半圆的中点,
左侧半圆的中点,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,
,![]()
![]() ,
,![]() .
.
(1)当![]() 时, 求证:
时, 求证:![]() .
.
(2)若![]() 的半径为
的半径为![]() ,请填空:
,请填空:
①当四边形![]() 为正方形时,
为正方形时,![]()
②当![]() 时, 四边形
时, 四边形![]() 为菱形.
为菱形.

【答案】(1)证明见解析;(2)①2;②22.5°
【解析】
(1)由切线性质和垂径定理可证明![]() ,从而可得四边形
,从而可得四边形![]() 是平行四边形,利用平行四边形性质即可证明结论;
是平行四边形,利用平行四边形性质即可证明结论;
(2)①根据正方形性质得到P点与O点重合即可得到答案;
②由点![]() 为
为![]() 的中点,可得
的中点,可得![]() ,由菱形性质易求
,由菱形性质易求![]() ,进而可求
,进而可求![]() .
.
解(1)证明:连接![]() ,
,
![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的半径,
的半径,
![]() ,
,
![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
(2)①当四边形![]() 为正方形时, BP=DQ,DP⊥AB,即P点与O点重合,
为正方形时, BP=DQ,DP⊥AB,即P点与O点重合,
∴DQ=BP=BO,
又∵![]() ,
,
∴![]() ,
,
故答案为:2;
②如图,连接BD,
∵点![]() 是
是![]() 左侧半圆的中点,
左侧半圆的中点,
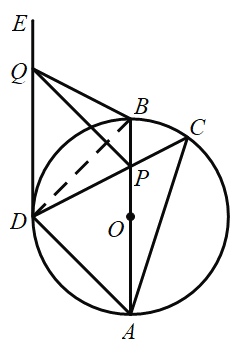
∴![]() ,
,![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
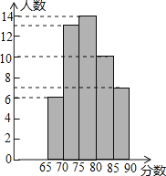
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.