Question

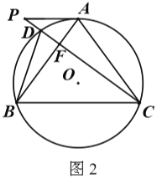
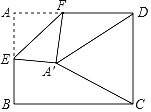
【题目】如图，在Rt△ABC中，AC＝BC＝4，∠ACB＝90°，正方形BDEF的边长为2，将正方形BDEF绕点B旋转一周，连接AE、BE、CD．

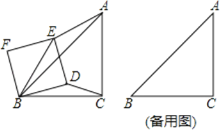
(1)请找出图中与△ABE相似的三角形，并说明理由；

(2)求当点E在线段AF上时CD的长；

(3)设AE的中点为M，连接FM，试求FM长的取值范围．

Answer 1

【答案】(1)证明见详解；(2)； (3)．

【解析】

（1）根据等腰三角形的性质和相似三角形的判定可以判断△ABE∽△CBD．

（2）根据相似三角形的性质得到AB=BC=，根据勾股定理得AF===，如图1，E在线段AF上，AE=AF－EF=，从而求出CD的长．

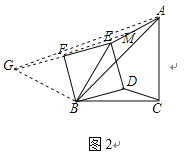
（3）如图2，延长EF到G，使FG=EF，连接AG，BG，求得△BFG是等腰直角三角形，得到BG=BF=，设M为AE的中点，连接MF，根据三角形中位线定理得到AG=2FM，根据三角形的三边关系即可得出结论．

解：（1）△ABE∽△CBD，

∵在Rt△ABC中，AC＝BC＝4，∠ACB＝90°，

∴∠ABC＝∠EBD＝45°，

∴∠ABE＝∠CBD，

∵＝，＝，

∴ ，

∴△ABE∽△CBD；

（2）∵△ABE∽△CBD，

∴＝＝ ，

∴CD＝AE，

∵AC＝BC＝4，∠ACB＝90°，

∴AB＝BC＝ ，

∵当点E在线段AF上时CD的长，

∵∠AFB＝90°，

∴AF===，

如图1，AE＝AF﹣EF＝﹣2，

∴CD＝﹣；

所以CD的长为﹣．

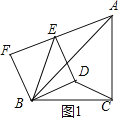
（3）如图2，延长EF到G使FG＝EF，连接AG，BG，则△BFG是等腰直角三角形，

∴BG＝BF＝，

设M为AE的中点，

连接MF，

∴MF是△AGE的中位线，

∴AG＝2FM，

在△ABG中，∵AB﹣BG≤AG≤AB+BG，

∴≤AG≤，

∴≤FM≤．