题目内容
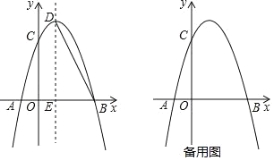
【题目】如图,开口向下的抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上的一点.
是第一象限内抛物线上的一点.
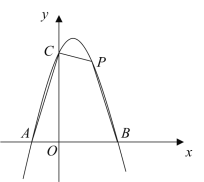
(1)求该抛物线所对应的函数解析式;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)8
;(2)8
【解析】
(1)设二次函数表达式为![]() ,再将点C代入,求出a值即可;
,再将点C代入,求出a值即可;
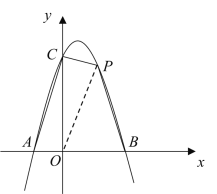
(2)连接OP,设点P坐标为(m,![]() ),m>0,利用S四边形CABP=S△OAC+S△OCP+S△OPB得出S关于m的表达式,再求最值即可.
),m>0,利用S四边形CABP=S△OAC+S△OCP+S△OPB得出S关于m的表达式,再求最值即可.
解:(1)∵A(-1,0),B(2,0),C(0,4),
设抛物线表达式为:![]() ,
,
将C代入得:,
解得:a=-2,
∴该抛物线的解析式为:![]() ;
;
(2)连接OP,设点P坐标为(m,![]() ),m>0,
),m>0,
∵A(-1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=![]()
=![]()
当m=1时,S最大,且为8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
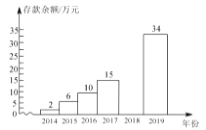
【题目】小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
收入 | 3 | 8 | 9 |
| 14 | 18 |
支出 | 1 | 4 | 5 | 6 |
| 6 |
存款余额 | 2 | 6 | 10 | 15 |
| 34 |
(1)表格中![]() ________;
________;
(2)请把下面的条形统计图补充完整:(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?