题目内容
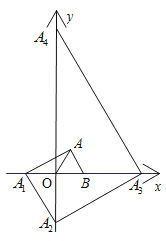
【题目】已知:如图,在平面直角坐标系中,点B的坐标为(1,0),以OB为边,在第一象限内作等边三角形OAB,过点A作AB的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交x轴于点
的垂线,交x轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线,交y轴于点
的垂线,交y轴于点![]() ,…,这样一直作下去,则点
,…,这样一直作下去,则点![]() 的坐标为______.
的坐标为______.
【答案】(![]() ,0)
,0)
【解析】
分别写出A1、A2、A3、A4的坐标找到变化规律后写出答案即可.
∵△AOB为等边三角形,且点B的坐标为(1,0),
∴∠ABO=∠AOB=60![]() ,OB=BA=OA=1,
,OB=BA=OA=1,
∵![]() ,
,
∴∠![]() ,
,
∴∠![]() ,
,
∴∠![]() ∠
∠![]() ,
,
∴![]() ,
,
∴![]() 的坐标为(-1,0),
的坐标为(-1,0),
在Rt△![]() 中,∠
中,∠![]() ∠
∠![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的坐标为(0,
的坐标为(0,![]() ),
),
同理:![]() ,
,
∴![]() 的坐标为(3,
的坐标为(3,![]() ),
),
同理:![]() ,
,
∴![]() 的坐标为(0,
的坐标为(0,![]() ),
),
…
∵2019÷4=504…3,
∴![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,
且![]() ,
,
∴![]() 的坐标为(
的坐标为(![]() ,
,![]() ) .
) .
故答案为:(![]() ,
,![]() )
)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
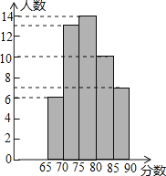
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.