题目内容
【题目】问题探究:
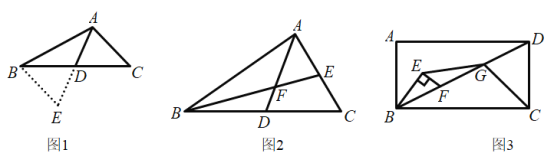
小红遇到这样一个问题:如图1,![]() 中,
中,![]() ,
,![]() ,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使
,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使![]() ,连接BE,证明
,连接BE,证明![]() ,经过推理和计算使问题得到解决.
,经过推理和计算使问题得到解决.
请回答:(1)小红证明![]() 的判定定理是:__________________________________________;
的判定定理是:__________________________________________;
(2)AD的取值范围是________________________;
方法运用:
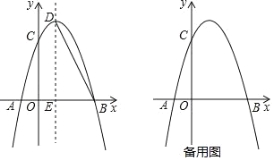
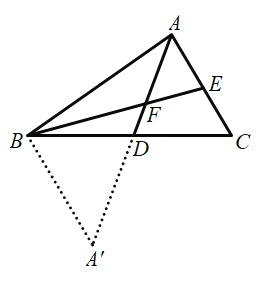
(3)如图2,AD是![]() 的中线,在AD上取一点F,连结BF并延长交AC于点E,使
的中线,在AD上取一点F,连结BF并延长交AC于点E,使![]() ,求证:
,求证:![]() .
.
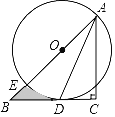
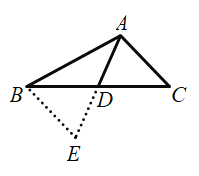
(4)如图3,在矩形ABCD中,![]() ,在BD上取一点F,以BF为斜边作
,在BD上取一点F,以BF为斜边作![]() ,且
,且![]() ,点G是DF的中点,连接EG,CG,求证:
,点G是DF的中点,连接EG,CG,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)见解析
;(3)见解析;(4)见解析
【解析】
(1)利用三角形的中线与辅助线条件,直接证明![]() ,从而可得证明全等的依据;
,从而可得证明全等的依据;
(2)利用全等三角形的性质得到![]() 求解
求解![]() 的范围,从而可得答案;
的范围,从而可得答案;
(3)延长![]() 至点
至点![]() ,使
,使![]() ,证明
,证明![]() ,利用全等三角形的性质与
,利用全等三角形的性质与![]() ,证明
,证明![]() ,得到
,得到![]() ,从而可得答案;
,从而可得答案;
(4)延长![]() 至点
至点![]() 使
使![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,证明
,证明![]() ,得到
,得到![]() ,利用锐角三角函数证明
,利用锐角三角函数证明![]() ,再证明
,再证明![]() ,利用相似三角形的性质可得
,利用相似三角形的性质可得![]() 是直角三角形,从而可得答案.
是直角三角形,从而可得答案.
解:(1)如图,AD是中线,
![]()
在![]() 与
与![]() 中,
中,
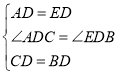
![]()
故答案为:![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
故答案为:![]()
(3)证明:延长![]() 至点
至点![]() ,使
,使![]() ,
,
∵![]() 是
是![]() 的中线
的中线
∴![]()
在![]() 和
和![]() 中
中
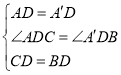
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,
,
又∵![]()
∴![]()
(4)证明:延长![]() 至点
至点![]() 使
使![]() ,连接
,连接![]() 、
、![]() 、
、![]()
∵G为![]() 的中点
的中点
∴![]()
在![]() 和
和![]() 中
中
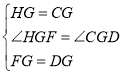
∴![]()
∴![]()
在![]() 中,∵
中,∵![]() ,
,
∴![]()
又矩形![]() 中,
中,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() 为
为![]() 的外角,
的外角,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,
![]()
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∵G为![]() 的中点,
的中点,
∴![]() ,
,
即![]() .
.

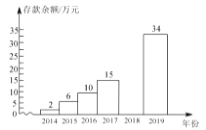
【题目】小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
收入 | 3 | 8 | 9 |
| 14 | 18 |
支出 | 1 | 4 | 5 | 6 |
| 6 |
存款余额 | 2 | 6 | 10 | 15 |
| 34 |
(1)表格中![]() ________;
________;
(2)请把下面的条形统计图补充完整:(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?